A raíz de una consulta recibida por parte de un cliente en la que se cuestionaba la aparición de esfuerzos de torsión en los soportes de un modelo de un puente curvo introducido en STATIK, hemos creído interesante compartir la respuesta con todos los usuarios.
Vimos que, en el modelo recibido, las pilas del puente tenían una orientación que no se correspondía con el eje del mismo. Este aspecto es fundamental, ya que la primera de las razones de que aparezcan torsiones en las pilas es que ninguno de los ejes principales de la sección sea coincidente con el eje del tablero, observándose de este modo un efecto obvio en la flexión como consecuencia de las diferencias de rigidez a flexión para cada eje de la sección.
Esto lo vemos rápidamente si introducimos un modelo muy sencillo de un puente de planta recta y vamos jugando con los giros de las pilas.

En la figura anterior vemos que las secciones de las pilas y los apoyos están orientados en concordancia con el eje del tablero. Si obtenemos las reacciones para una carga horizontal según la directriz del tablero, cabe esperar que no aparezcan torsiones (Mz).
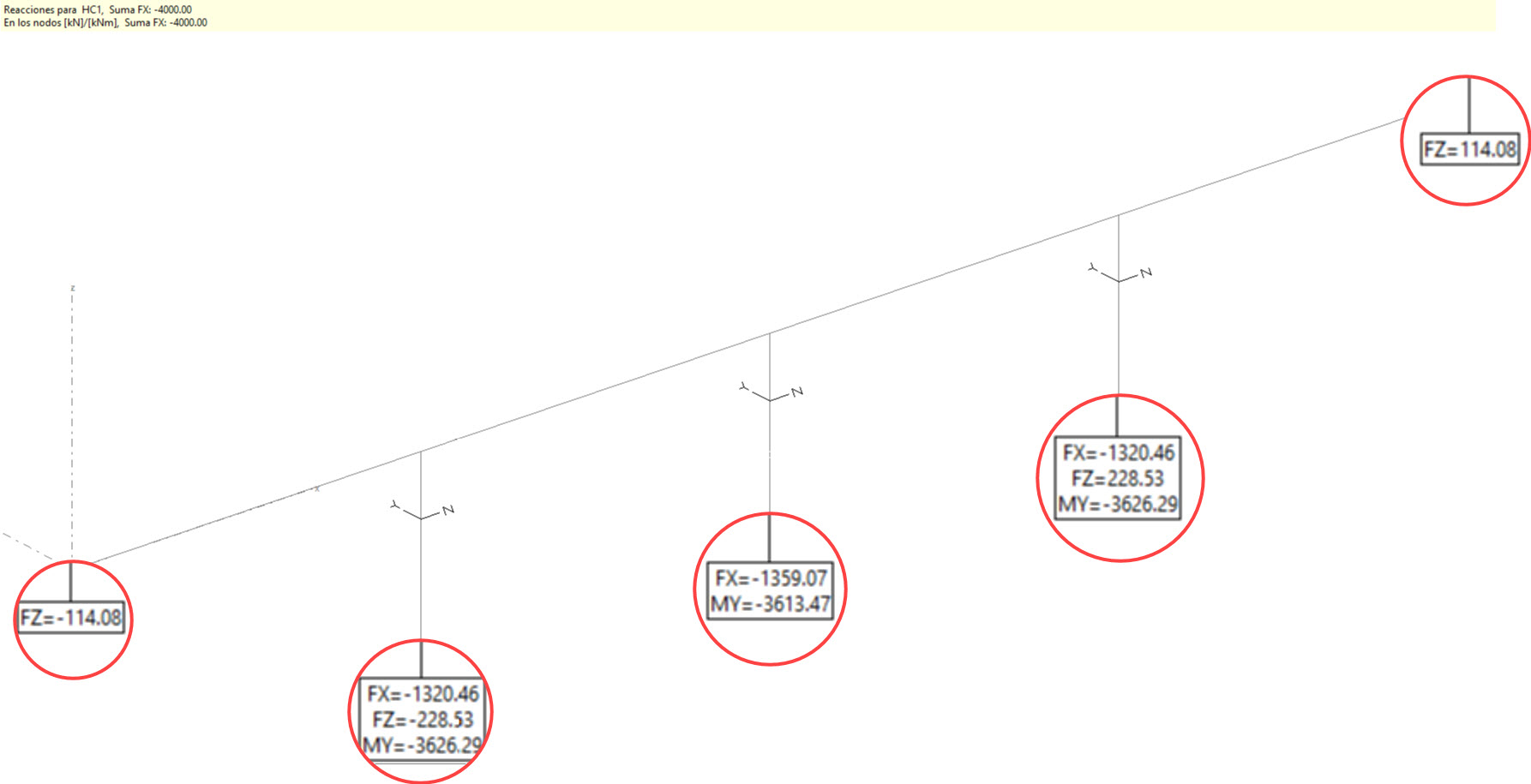
Efectivamente vemos que así es.
Vamos a girar las pilas por ejemplo 15 grados:

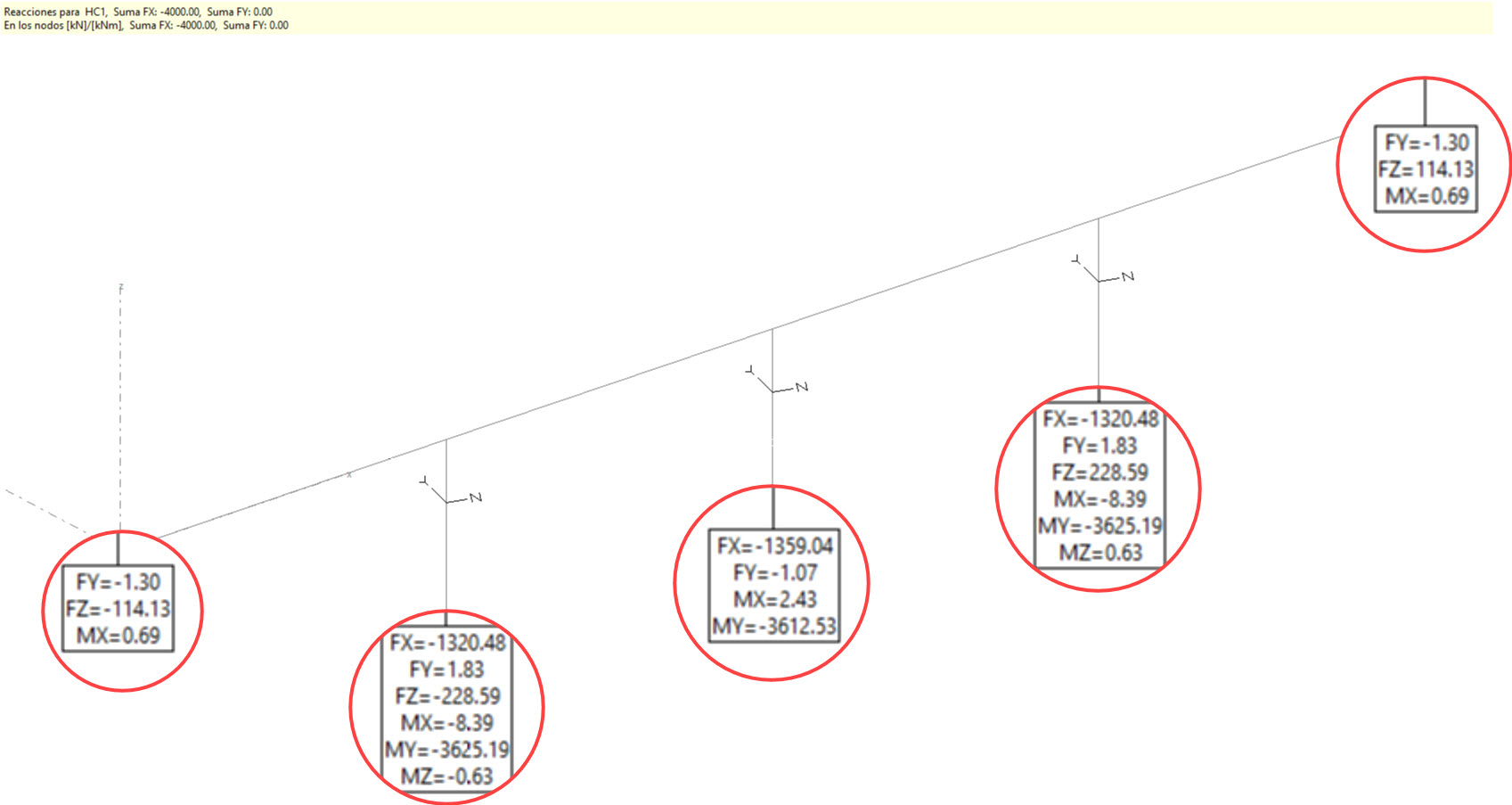
Inmediatamente comprobamos que aparecen torsores Mz.
Lo anterior ocurre siempre que las secciones de las pilas tengan distinto momento de inercia en cada uno de sus ejes, lo cual afectará a la matriz de rigidez de la estructura y, por lo tanto, en los resultados que se obtienen en la resolución del sistema de ecuaciones. Si la sección presenta el mismo momento de inercia en los dos ejes, el giro de las pilas no supone la aparición de torsores al ser simétrica la matriz de rigidez. Veámoslo asignándole una sección cuadrada a las pilas.

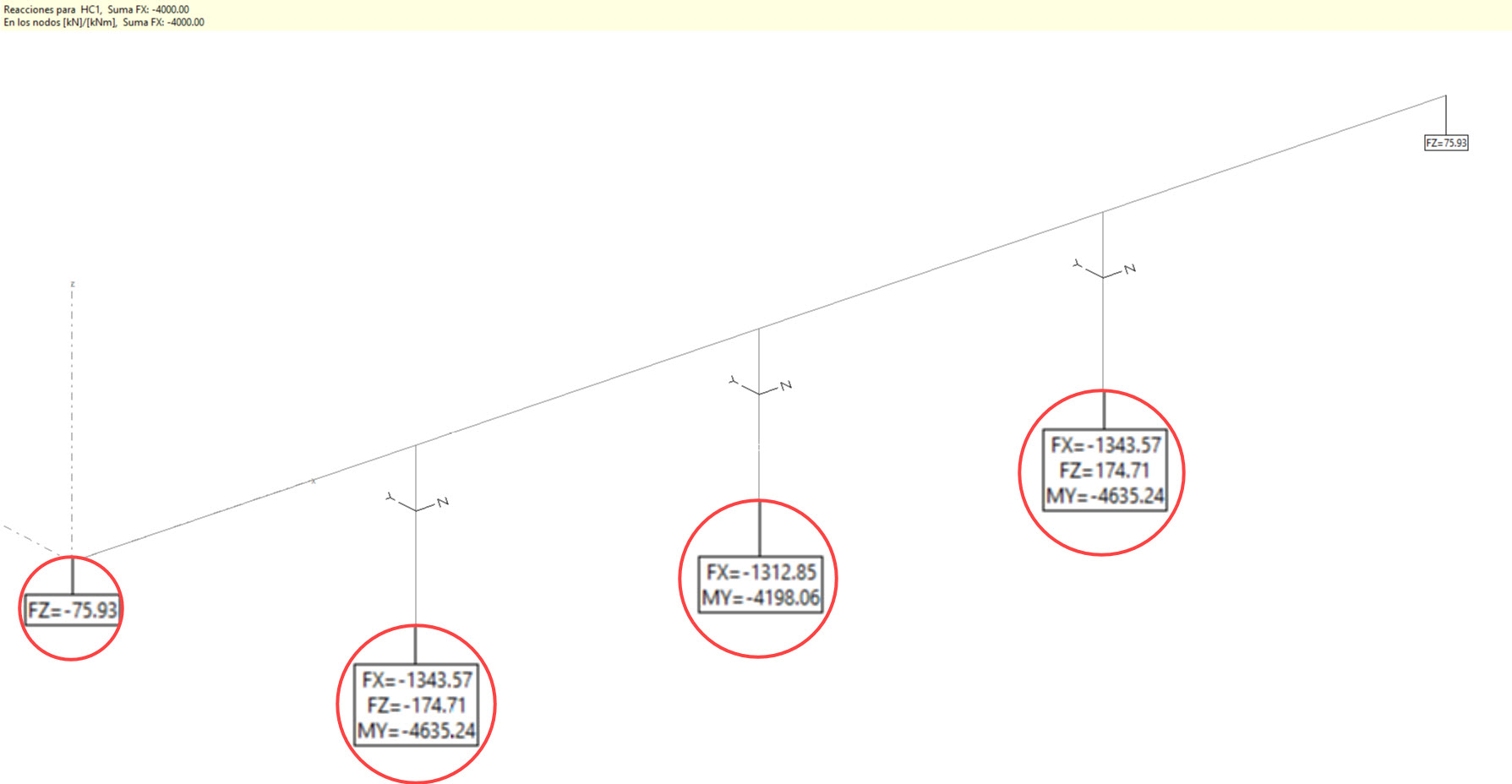
Si giramos las pilas:

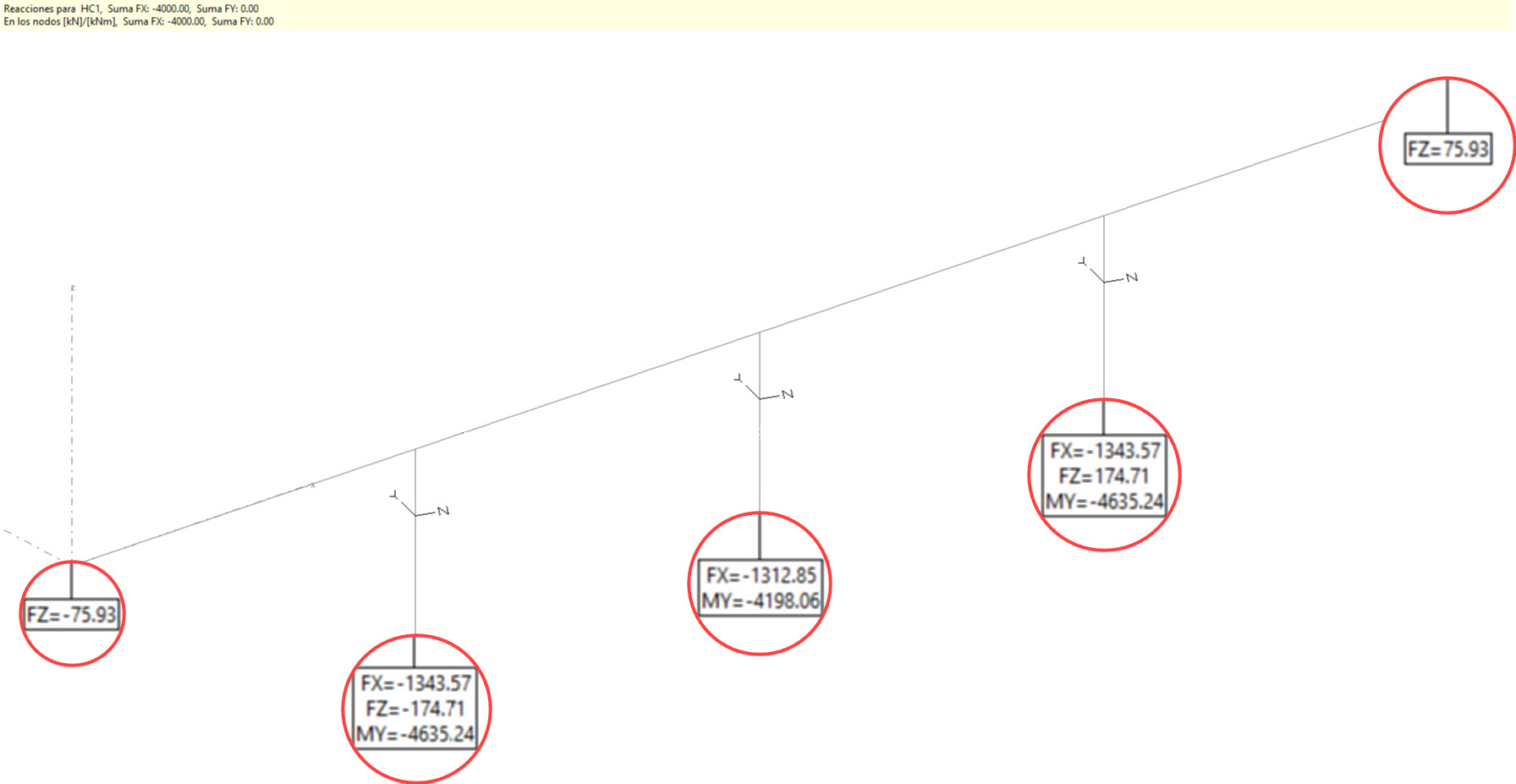
Vemos que tampoco aparecen torsores.
En un puente curvo, la aparición de torsiones en las pilas no sólo se debe a la orientación de las pilas, sino también a que las cargas en cualquier punto del tablero tendrán un excentricidad con respecto a las pilas, lo que tendrá como resultado un torsor en cada una de ellas. Veámoslo con un sencillo ejemplo en el que orientamos las pilas según el eje del tablero y aparecen torsiones:

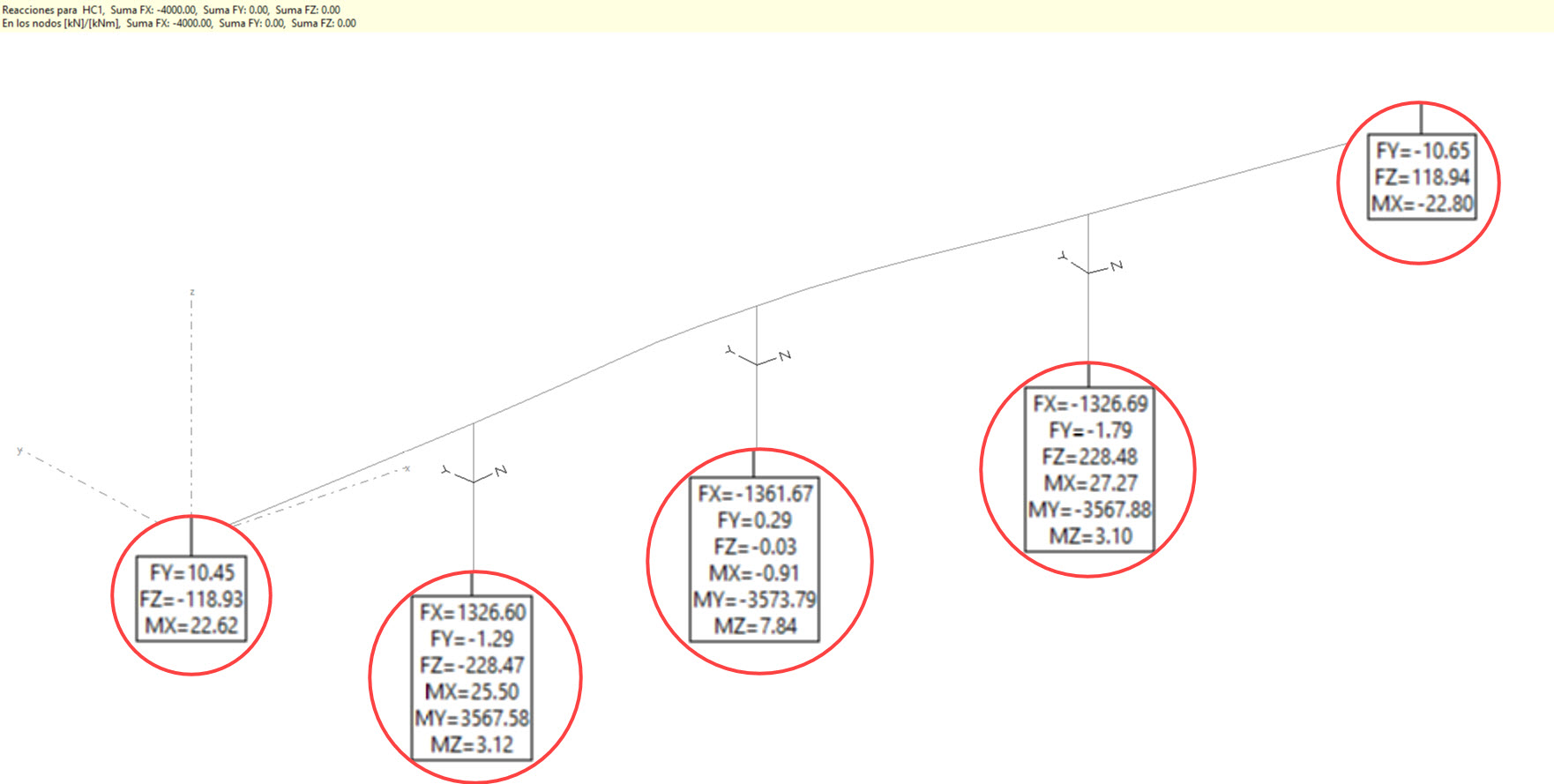
Finalmente nos gustaría comentar que también es importante que se tenga en cuenta la orientación de los apoyos introducidos, de manera que, por ejemplo en los extremos de un puente curvo, el desplazamiento según el eje X coincida con el eje del tablero:

Los apoyos suponen coacciones frente a los movimientos en unos determinados ejes. Si al editar las coacciones del apoyo permitimos que la superestructura que pasa por ese apoyo se pueda desplazar libremente según X, ¡¡tenemos que estar seguros de qué es X!!!. Además, incluso si bloqueamos todos los grados de libertad pero no giramos los apoyos, estaremos obteniendo unos resultados en unos ejes que, por defecto, corresponden a los ejes del sistema global de coordenadas y que no tienen por que coincidir con la orientación real de los elementos de soporte. Esto nos lleva a concluir que se debe prestar atención también a la orientación de los apoyos para que los resultados de las reacciones obtenidos sean coherentes con la orientación de las pilas y estribos, y que puedan servir, por ejemplo, para llevar a cabo el dimensionamiento de las zapatas.
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).


















