Con el diagrama My-N de FAGUS, podemos ver de forma gráfica y tabular todos los posibles estados límite, para una o varias cuantías de armadura que pueda tener nuestra sección.
Siendo más precisos, observamos los puntos que cumplen con unos parámetros de análisis determinados, que por lo general se corresponderán con un estado límite, pero pueden tener otras condiciones, como por ejemplo una tensión máxima en el acero determinada, de manera que las parejas de puntos M-N hacen que la tensión sea la dada.
Por lo general, como decimos, en este diagrama se están presentando, aquellos puntos My-N que agotan la sección (ELU), pero también existe una tercera variable que entra en juego en la determinación de la resistencia de las secciones a flexión. Esta tercera variable es el momento en Z (Mz) e implica que, en el espacio, existe una superficie formada por las combinaciones My-Mz-N que agotan la sección.
La cuestión que nos lleva a desarrollar este artículo es: ¿qué "corte" plano de esa superficie de estados límite nos está mostrando el diagrama My-N de FAGUS?
Como es lógico, la superficie de los estados límite de nuestra sección estará formada por infinitas combinaciones My-Mz-N. Para poder representar en un diagrama plano las parejas My-N que agotan la sección, habrá que fijar alguno de los parámetros que entran en juego. Este parámetro para FAGUS es la curvatura de la sección en Z (Χz), siendo así nuestros planos de deformación: curvatura en Y libre (Χy≠0) y curvatura en Z fija (Χz=0).
Obligar a que no haya curvatura en Z, hará que existan momentos en Z que deberán aparecer para compensar el giro de los ejes principales de la sección. Veámoslo.
Tomemos una sección no simétrica como la de la siguiente figura:
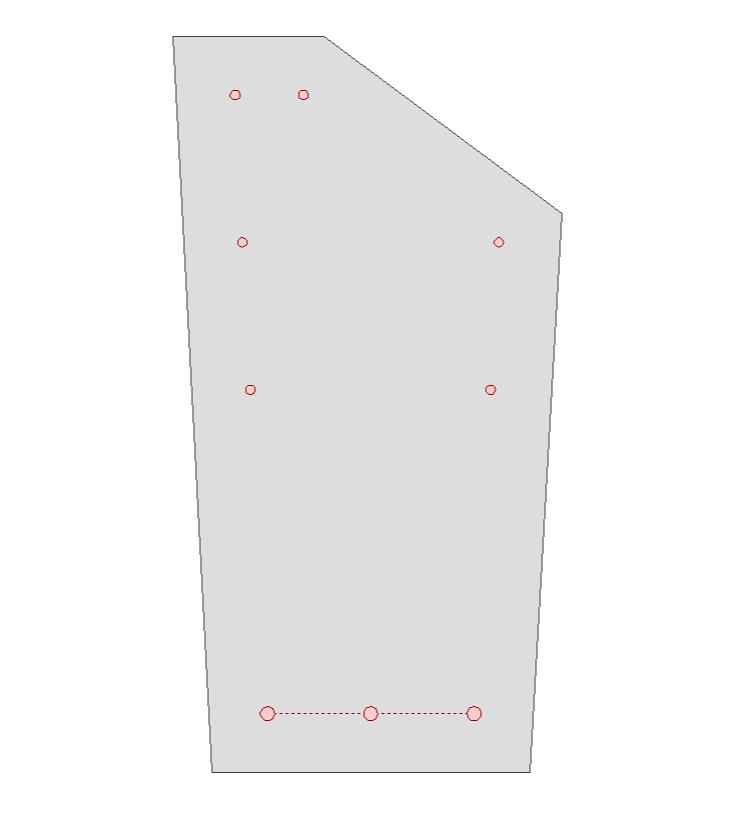
Si le pedimos a FAGUS que obtenga el diagrama My-N para esta sección y para la cuantía de armadura presente:
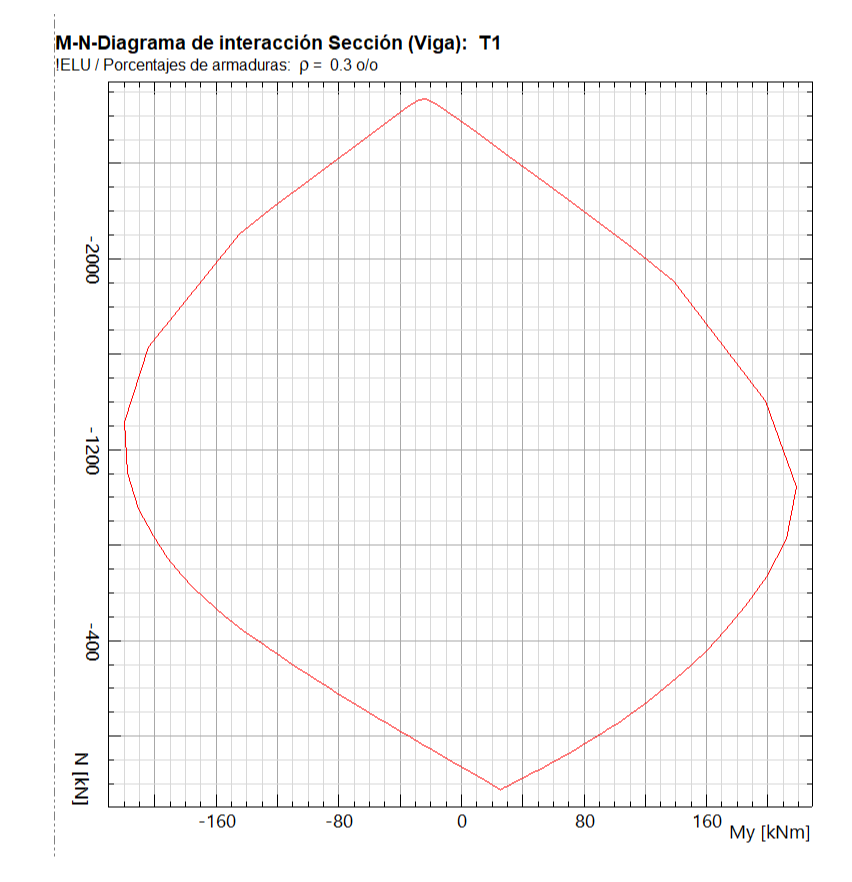
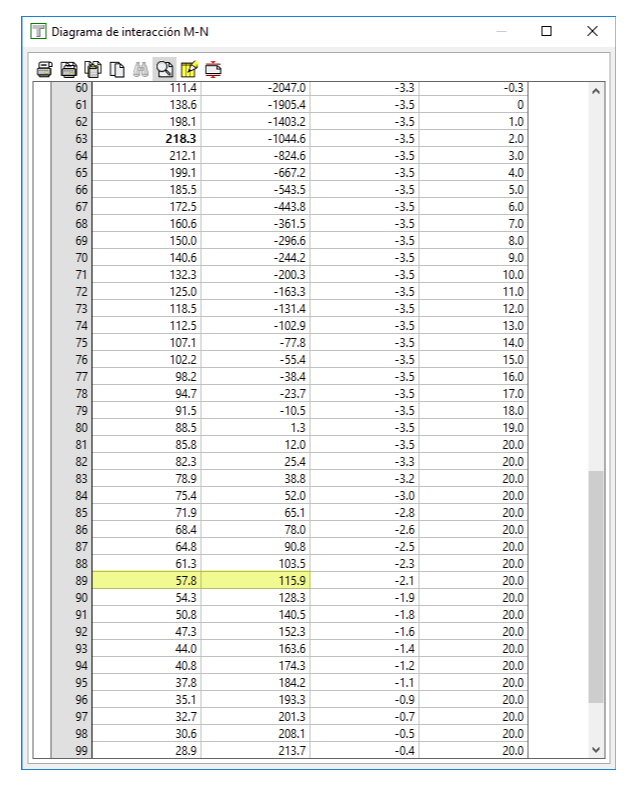
A priori, si tomamos cualquier punto de este diagrama y hacemos un análisis de eficiencia, deberíamos obtener una eficiencia igual a 1.00. Tomando al azar uno de los puntos del diagrama, por ejemplo el que indicamos en la figura siguiente, y suponiendo que Mz=0 (porque no aparecen valores de esta variable en el diagrama):
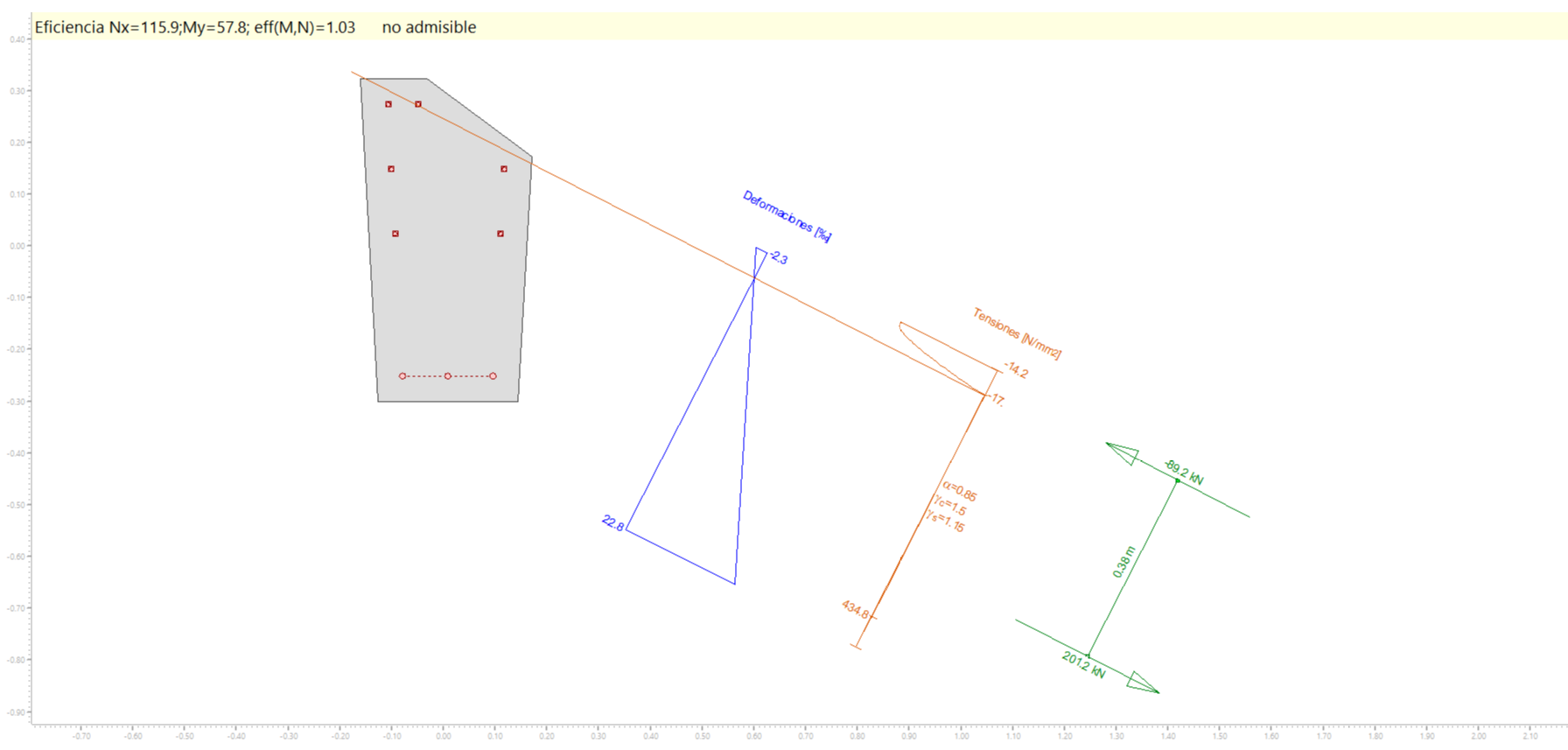
Vemos, en primer lugar, que la sección está girando respecto a un eje que no es horizontal. Este giro del eje es necesario para que la figura esté en equilibrio cuando se somete a los esfuerzos N y My introducidos.
Además, viendo los resultados numéricos, podemos comprobar que, en el estado límite último, el momento Mz sería cero y que la curvatura en Z sería distinta de cero:
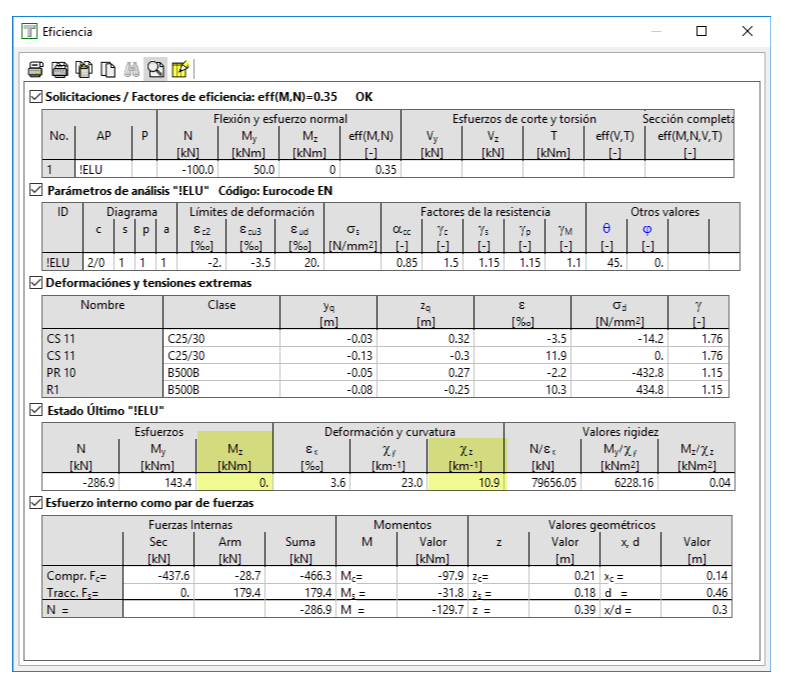
También vemos algo que sorprende: la eficiencia es 1.03>1.00, por lo que la terna de valores N=115.9 kN, My=57.8 kNm y Mz=0 kNm, que hemos introducido, no forma parte del diagrama (lo que implicaría una eficiencia de 1.00) sino que es exterior al mismo. Además, en la tabla anterior, vemos que los esfuerzos últimos no son los introducidos, tomados de los datos tabulares del diagrama. Si los valores de N y My introducidos fueran los esfuerzos en el estado límite último, serían los valores que veríamos en la tabla "Estado último !ELU" de arriba.
Esto se debe a que, en realidad, el diagrama nos está ocultando algo y es que el momento Mz último no es cero sino que tiene un valor.
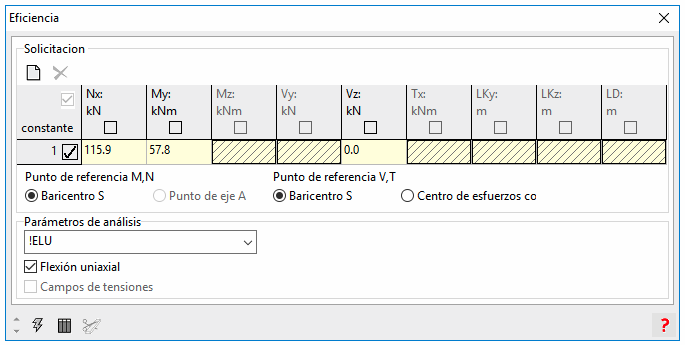
Este valor, como hemos visto, no se nos proporciona en los datos del diagrama, pero lo podemos obtener si forzamos a que el programa haga un análisis de eficiencia con flexión uniaxial, es decir, obligando a que la curvatura en Z sea cero.
Introduciendo los mismos valores N y My de antes, pero marcando la opción de "Flexión uniaxial":

Obtenemos, ahora sí, una eficiencia de 1.00 y vemos que el eje de giro de la sección es horizontal.
Si vemos los resultados numéricos:
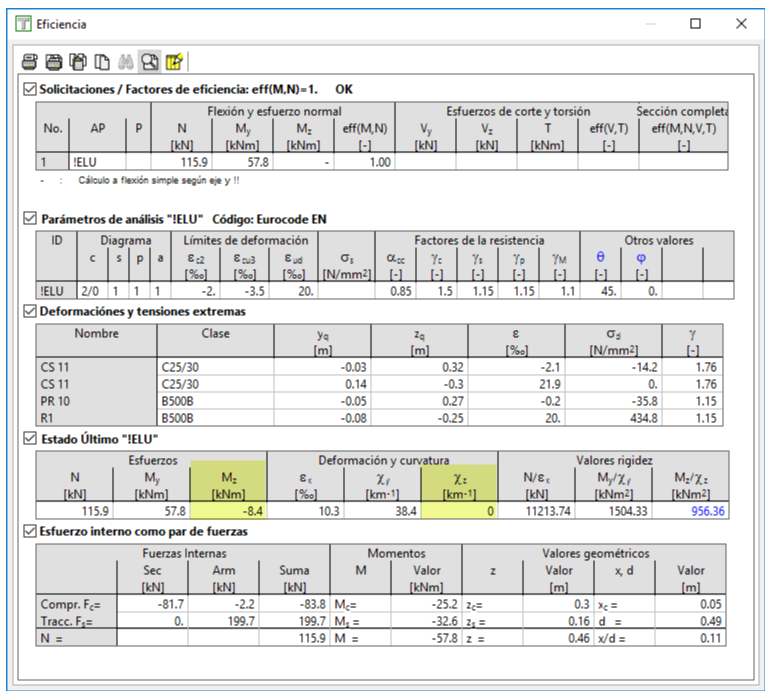
Vemos que aparece un momento Mz último de -8.4 kNm. Este momento es el que hace, junto con el My introducido, que la sección gire con respecto a un eje horizontal o, lo que es lo mismo, que la curvatura en Z sea cero, como también vemos en la tabla anterior.
Esto sería equivalente a hacer un análisis de eficiencia sin obligar a que sea con flexión uniaxial, pero introduciendo un Mz=-8.4 kNm:
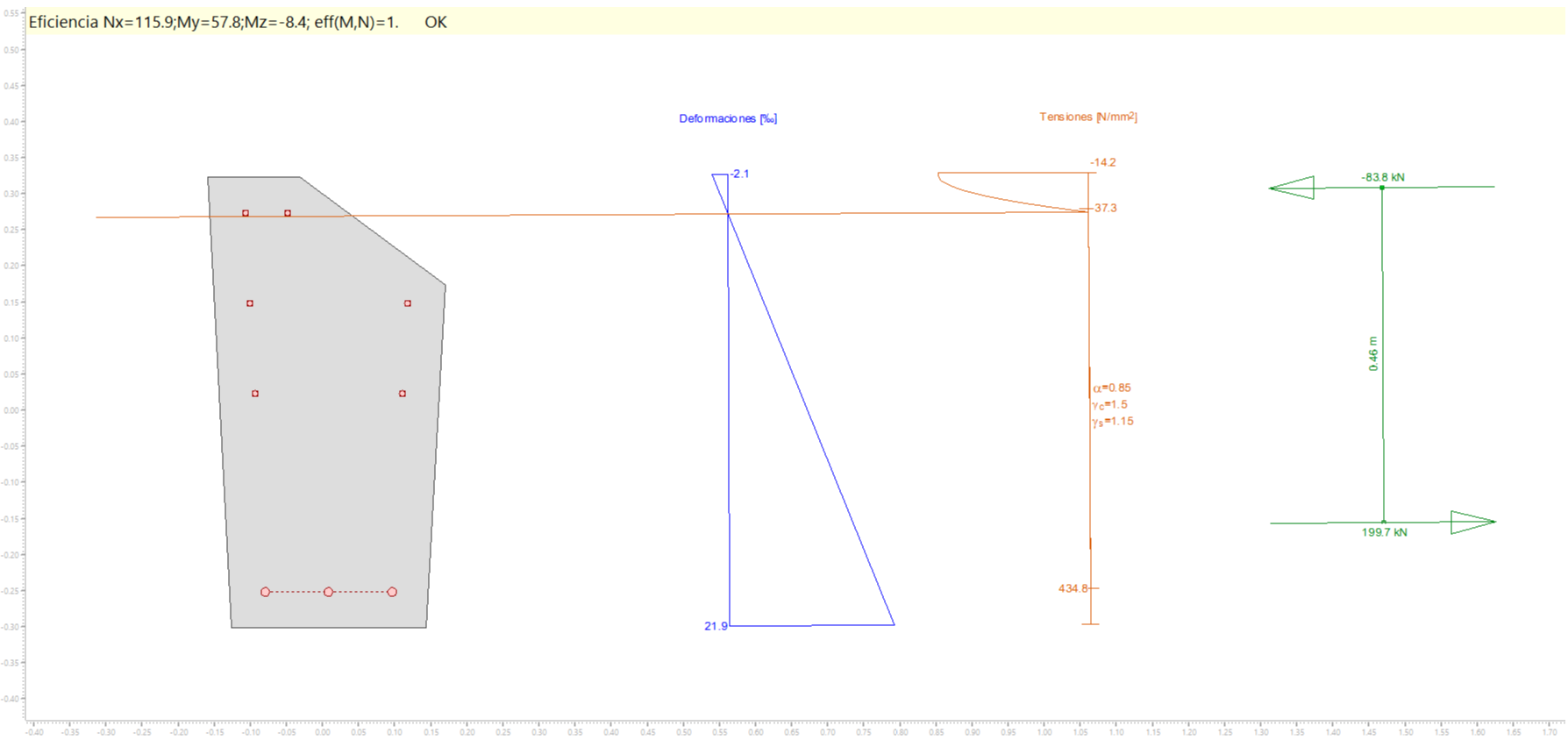
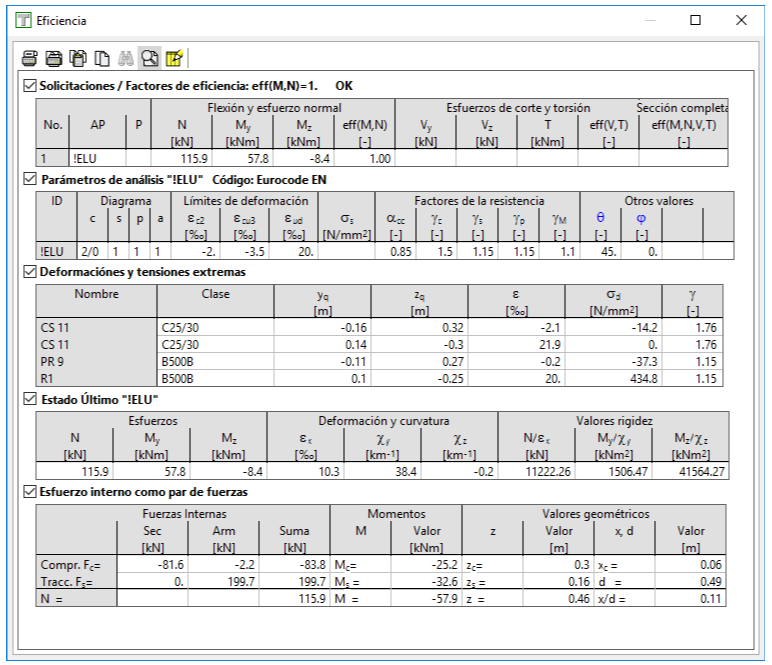
Como vemos, se obtienen los mismos resultados.
Como conclusión podemos decir que el diagrama de interacción My-N nos está presentando la proyección en el plano Mz=0 del conjunto de puntos que agotan la sección. Esos puntos pueden tener una coordenada Mz, que no nos va a mostrar, pero que únicamente existirá si tenemos una sección con geometría no simétrica, cuyo eje de giro no sea coincidente con el eje horizontal (eje Y). Si tenemos una sección simétrica (que será lo habitual), el plano de corte de la superficie en el espacio My-Mz-N coincidirá con el plano Mz=0 y, llevando a cabo un análisis de eficiencia con los esfuerzos correspondientes a cualquier punto del diagrama, obtendremos una eficiencia de 1.00.
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).

Quizás también te interese:

















