En este artículo queremos enseñaros cómo diseñar un depósito con geometría circular empleando el programa STATIK-8.
PLANTEAMIENTO DEL MODELO
Para desarrollar el modelo de la estructura nos basaremos en un emparrillado compuesto por elementos verticales, que se unirán transversalmente con elementos horizontales. Esta disposición de elementos generará un entramado de barras y nudos (ver figura inferior) que nos permitirá analizar su comportamiento frente a los distintos esfuerzos solicitantes típicos de una estructura con estas características. Para desarrollar este ejemplo, vamos a introducir un depósito circular de 10 metros de radio y 5 metros de altura de muro.
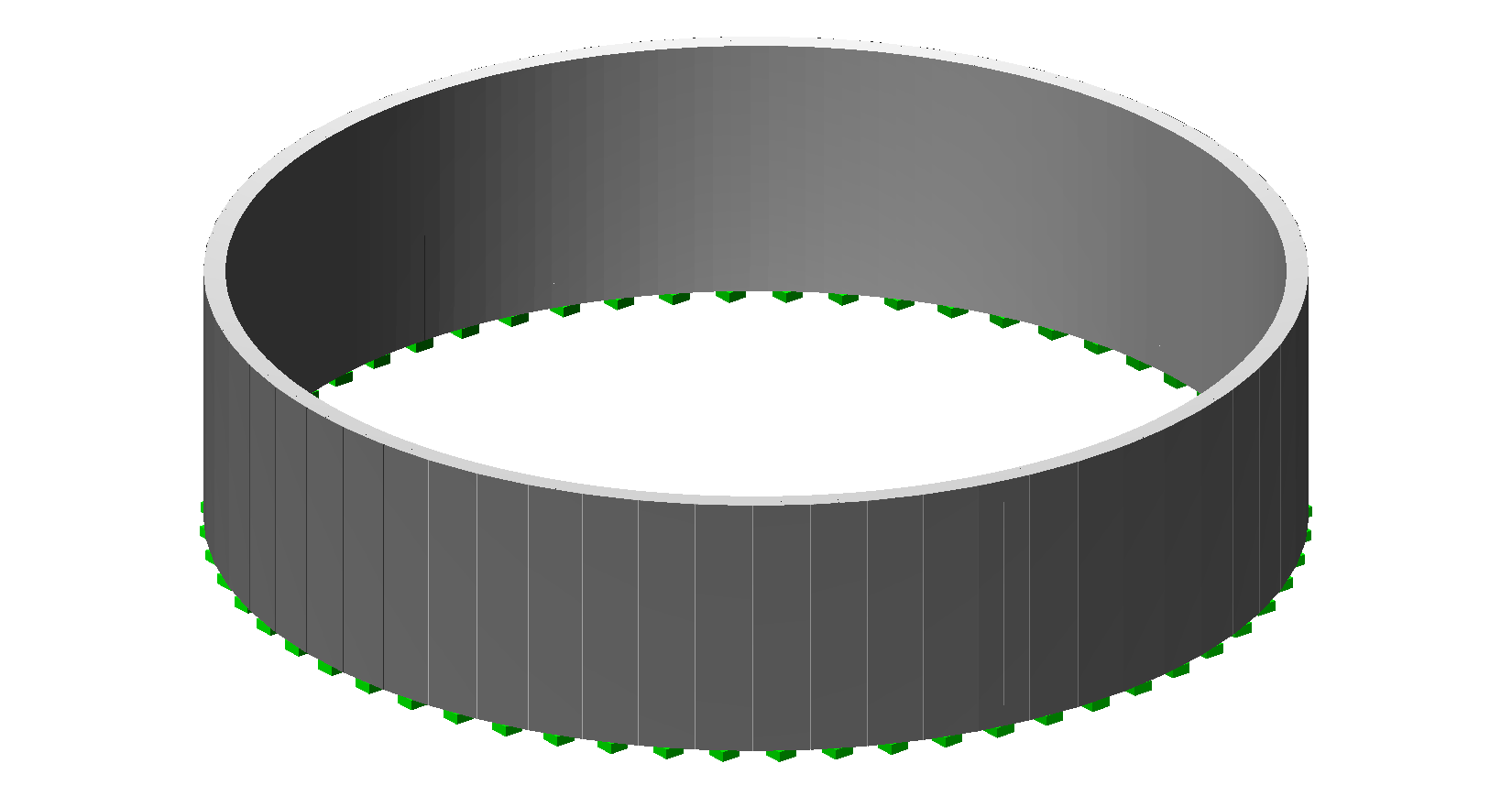
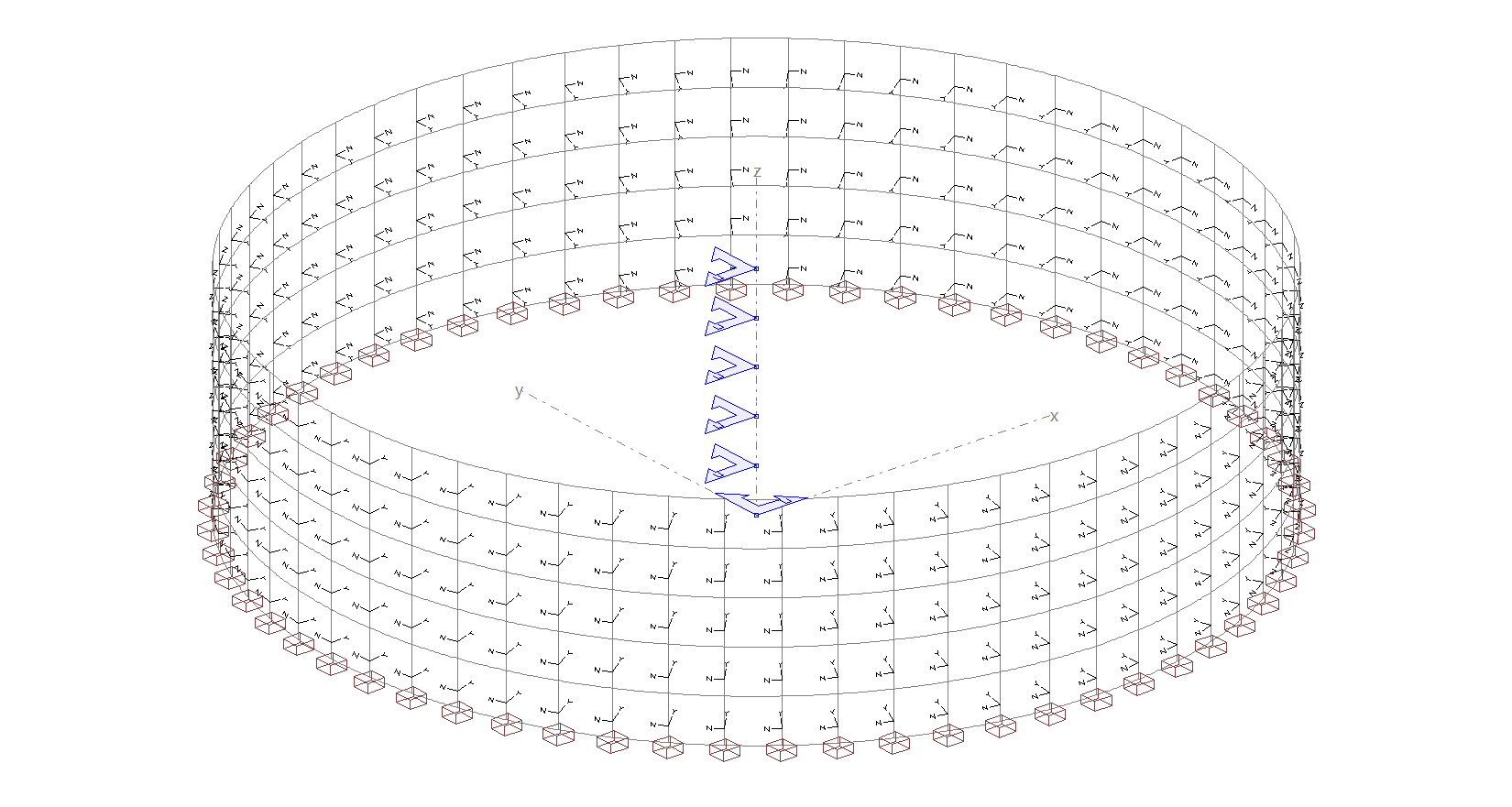
Un depósito circular puede ser de hormigón armado o pretensado y, dependiendo del caso en el que estemos, nos valdremos de unas herramientas de STATIK u otras.
Si tenemos un depósito de hormigón armado, el emparrillado estará compuesto por elementos tipo "barra" en ambas direcciones, vertical y horizontal.

Si tenemos un depósito en el que debamos un introducir tendones de pretensado, dispondremos elementos tipo "barra" en en vertical, pero la introducción de tendones requiere de la existencia de "líneas de estructura". Puesto que los tendones se disponen alrededor del depósito, las "líneas de estructura" conformarán los anillos de hormigón que conectarán las "barras" verticales para, posteriormente, asignar los tendones a ellas.

Desde el punto de vista de las cargas, deberemos obtener las cargas lineales equivalentes al empuje hidrostático del agua y que aplicaremos a cada una de las barras que constituirán los segmentos verticales del depósito. Estas cargas dependerán de la altura del depósito y del ancho de los segmentos en los que discreticemos el muro. Si el depósito es pretensado, tendremos además las cargas que introducen los tendones en nuestra estructura.
Finalmente, nos quedarían por definir los apoyos. Un depósito puede estar (generalmente) empotrado o articulado en su base y, en función de esta condición de apoyo, el comportamiento será distinto.
INTRODUCCIÓN DEL MODELO
Estructura
La introducción gráfica de un modelo en STATIK es muy sencilla y, en el caso de una estructura como la que nos ocupa, no es una excepción. El programa dispone de un conjunto de utilidades de dibujo que nos facilita esta tarea enormemente.
Para introducir los distintos elementos que componen nuestro emparrillado podemos adoptar dos vías: introducción gráfica directa en STATIK o introducción de los elementos basándonos en una plantilla en DXF. En este caso, vamos a explicar cómo hacerlo de forma directa.
Puesto que se trata de una estructura con planta circular deberemos, en primer lugar, tomar una importante decisión, en la que se basará toda la introducción del modelo y el posterior cálculo: ¿En cuántas secciones queremos discretizar el muro de nuestro depósito? De esto dependerá el ancho de las secciones de los elementos verticales y el valor de las cargas lineales equivalentes al empuje hidrostático que solicitará a cada uno de ellos.
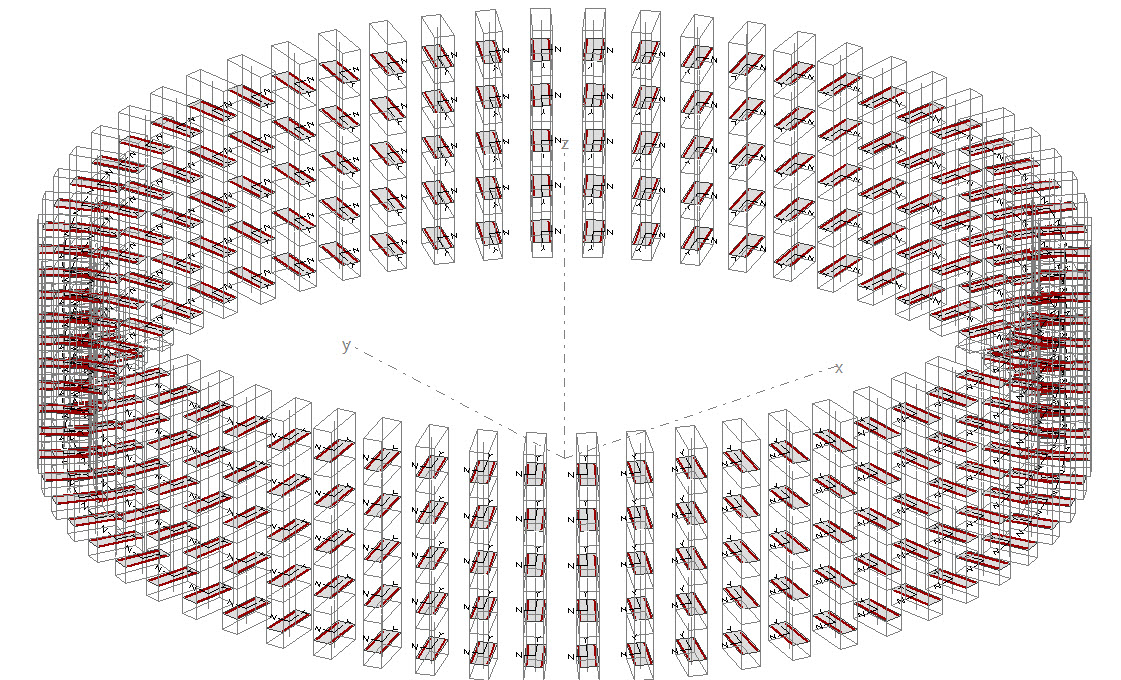
En el caso que nos ocupa hemos decidido discretizar el muro en 60 elementos verticales, lo que hace que cada una de ellos esté compuesto por una sección de 1.05m de ancho, que se obtiene directamente de dividir la longitud total de la circunferencia (L=2*pi*R=2*3.14*10=62.83m) entre 60. Además hemos tomado un espesor del muro de 0.4m. Definimos, por lo tanto, una sección con estas dimensiones, que posteriormente asignaremos a cada elemento vertical:
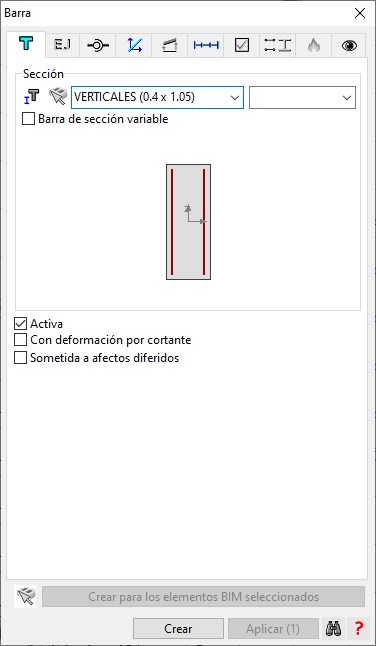
Puesto que la altura del muro es de 5m, vamos a dividir cada elemento vertical en 5 barras de 1m de longitud. De este modo conseguiremos tener un nudo del emparrillado a cada metro, que nos vendrá muy bien a la hora de introducir los elementos horizontales.
Con todo lo anterior, vamos a ir detallando cada paso para introducir nuestra geometría:
1) Dibujar una línea auxiliar de de 10m de longitud desde el punto central de nuestra circunferencia. Esto nos definirá el punto en el que introduciremos nuestro primer elemento vertical.
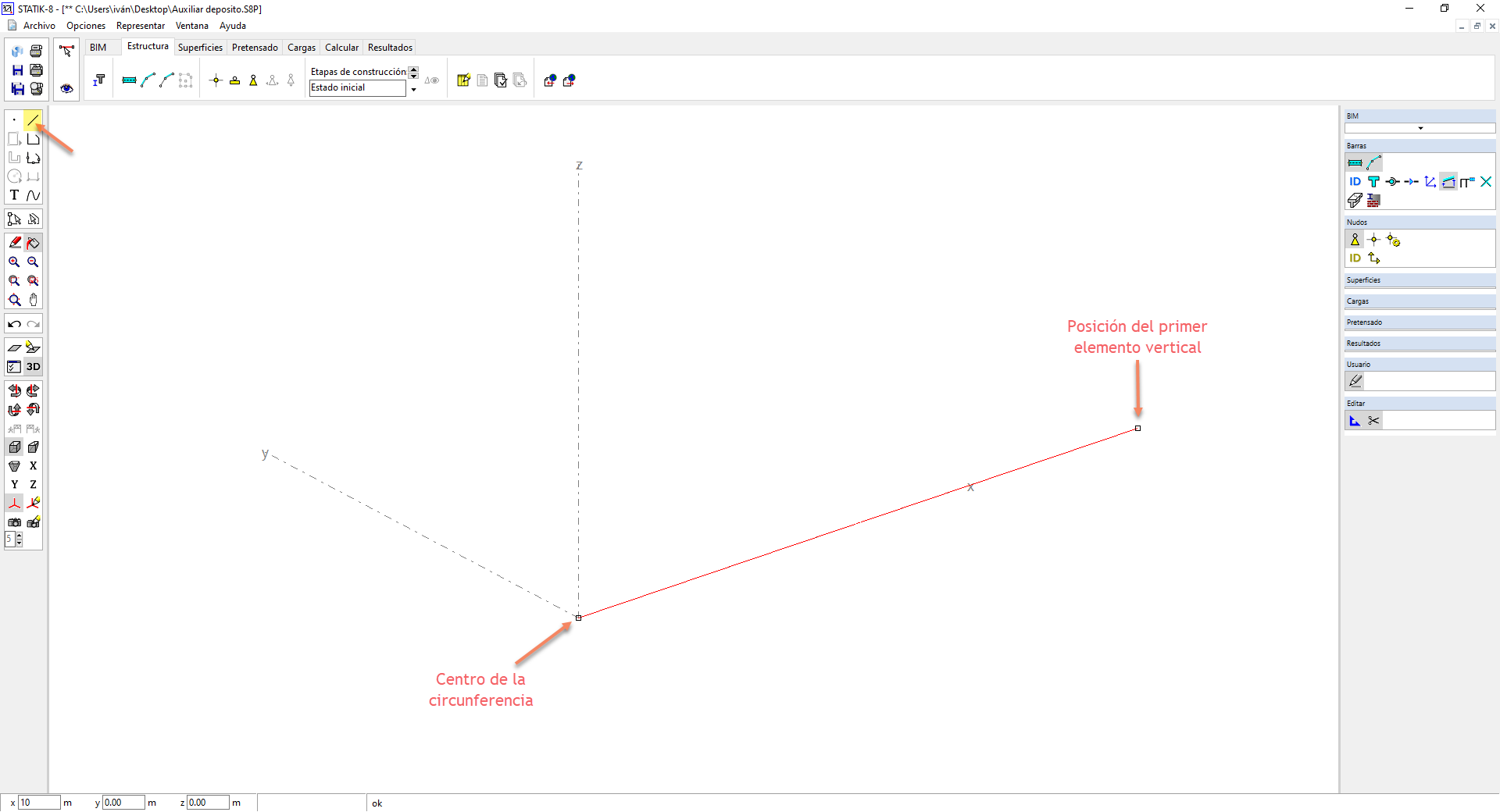
2) Introducción del primer elemento vertical (barra con sección definida) en el punto indicado y discretización en 5 barras de 1m de longitud.
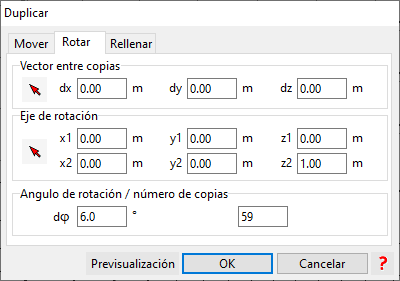
3) Replicamos el elemento vertical 59 veces (para tener 60 en total, como hemos dicho anteriormente) utilizando la herramienta de duplicar rotando:
En el cuadro de diálogo deberemos especificar 3 datos: el eje de rotación (eje Z global en este caso), el ángulo de rotación (6º en este caso, que se obtienen de dividir 360º/60 segmentos) y número de copias (59).
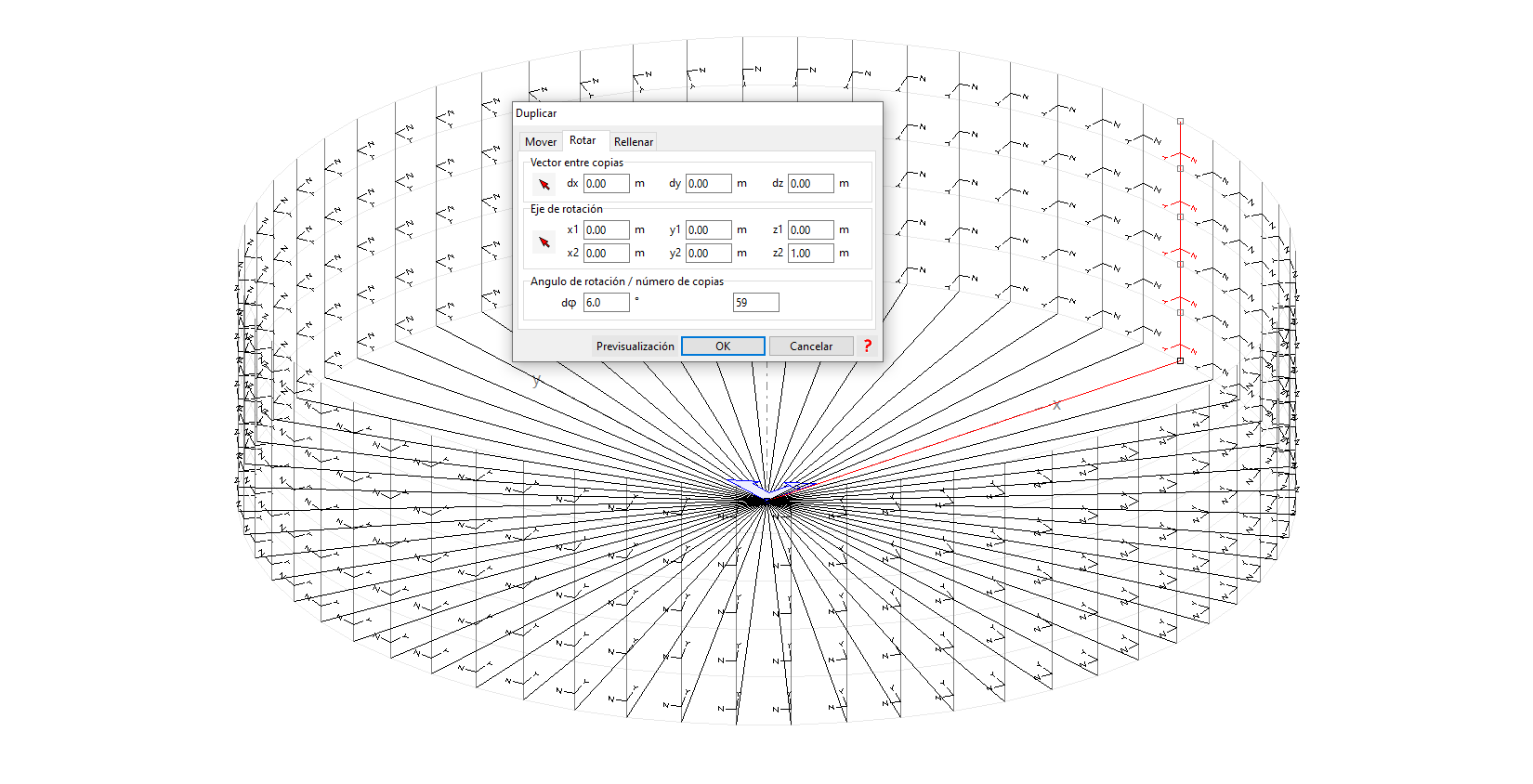
4) Cuando se copian elementos de esta forma nos encontramos con un pequeño detalle que hay que corregir para que nuestra estructura quede perfectamente introducida. Este detalle son los ejes locales de cada una de las barras.
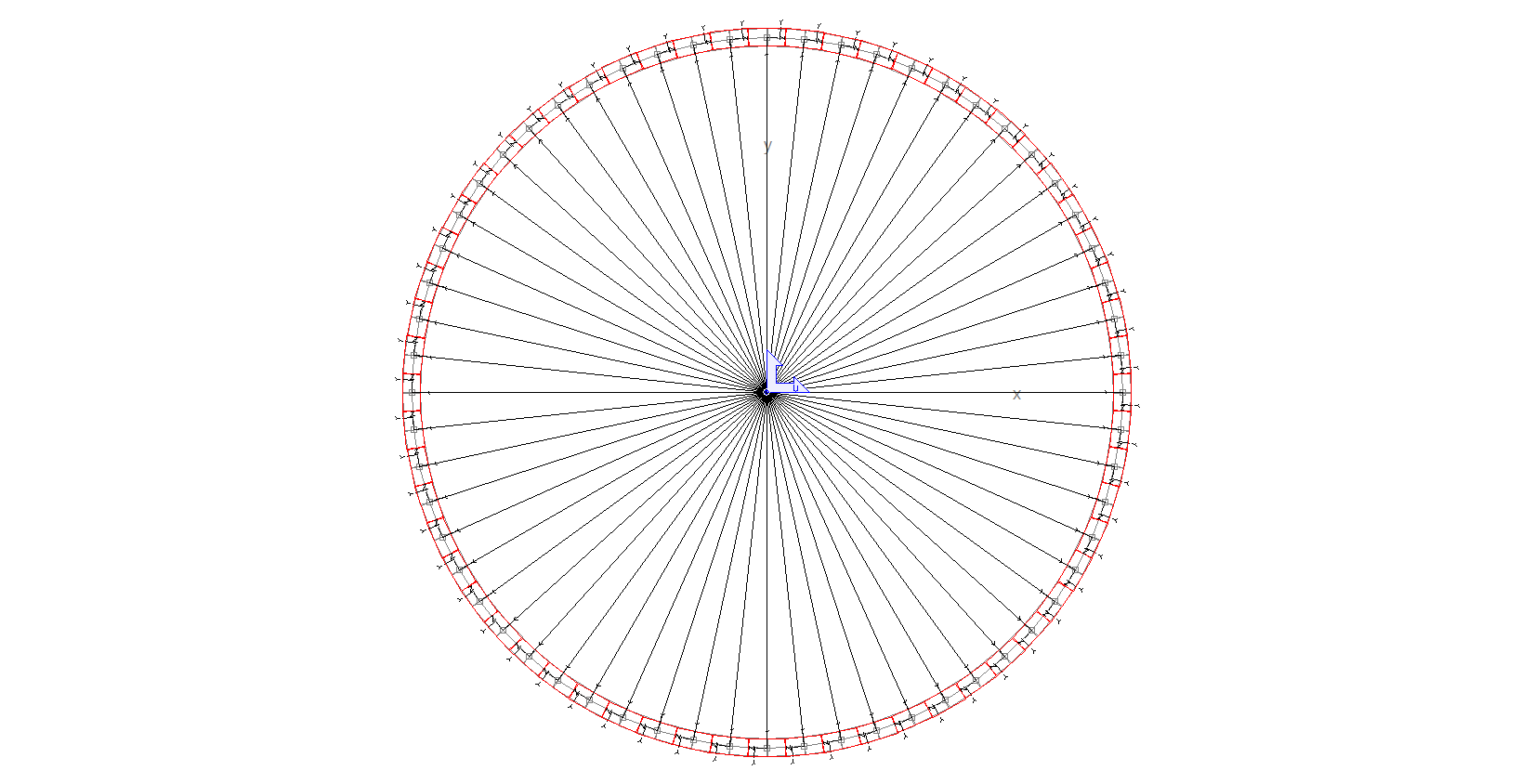
Si no hacemos nada, la orientación de los ejes locales de todas las barras será la de las barras originales, como puede verse en la siguiente figura:
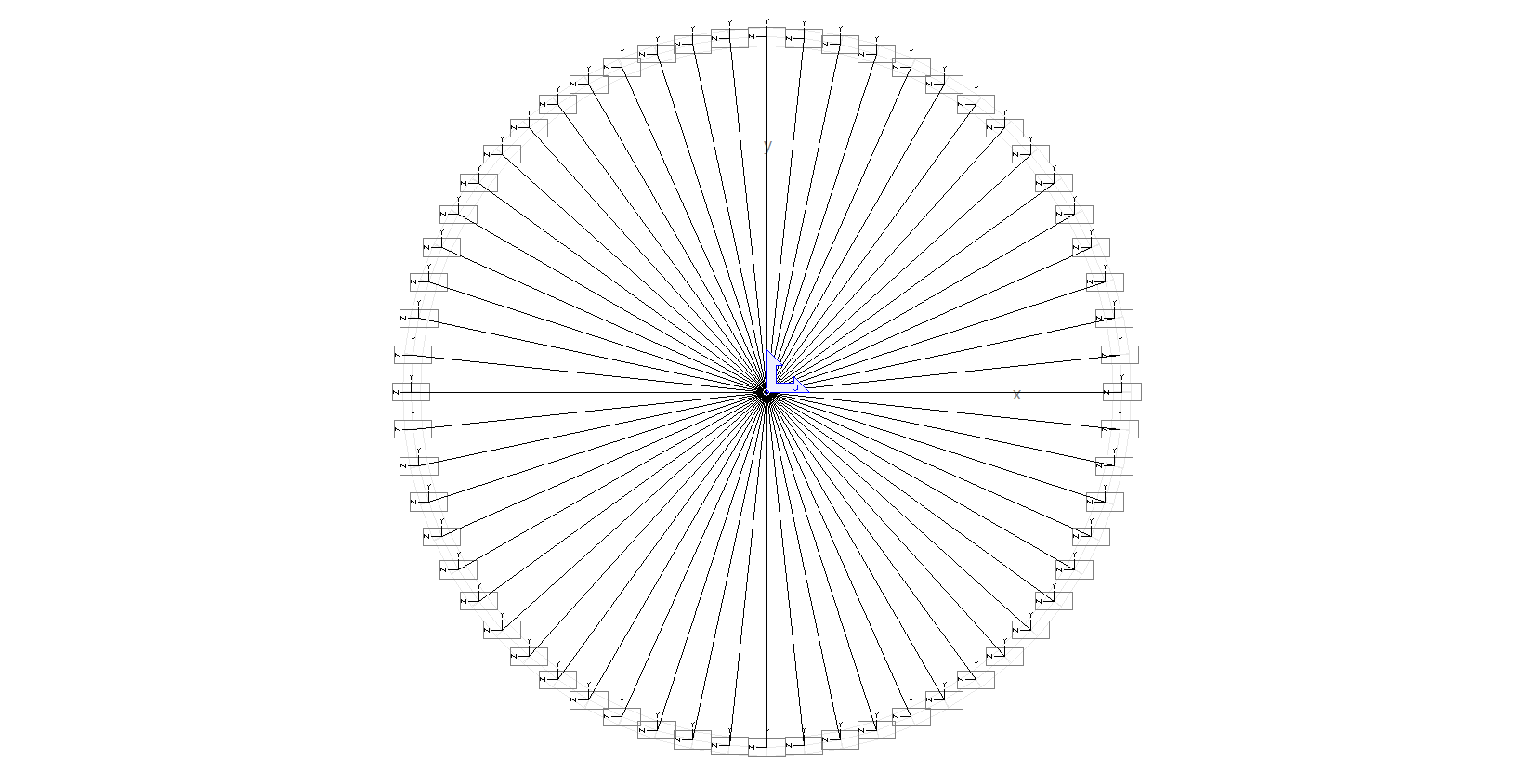
Esto se soluciona de una forma muy sencilla mediante la cuarta pestaña del cuadro de diálogo "Atributos" de las barras. Originalmente las opciones estarán seleccionadas de la siguiente forma:
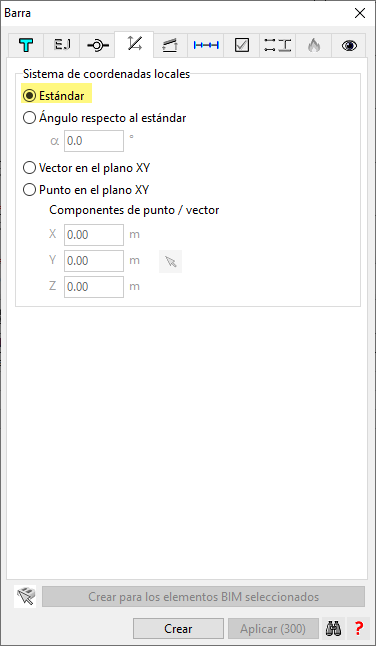
Para orientar los ejes de forma que todas nuestras barras "apunten" hacia el centro de la circunferencia, bastará con indicarlo de la siguiente forma (es muy importante conocer las coordenadas del punto en cuestión, que es nuestro caso es el (0,0,0)). De esta forma, si el (0,0,0) está en el plano XY de todos los sistemas locales de coordenadas, tendremos el problema resuelto.
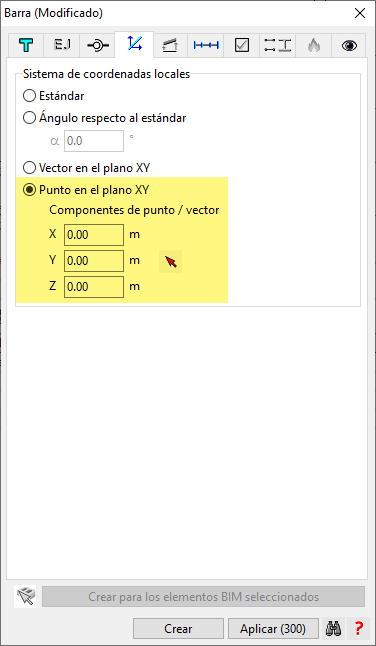
Aplicando esta opción a todas las barras, ya las tendremos como nos interesa en este caso:
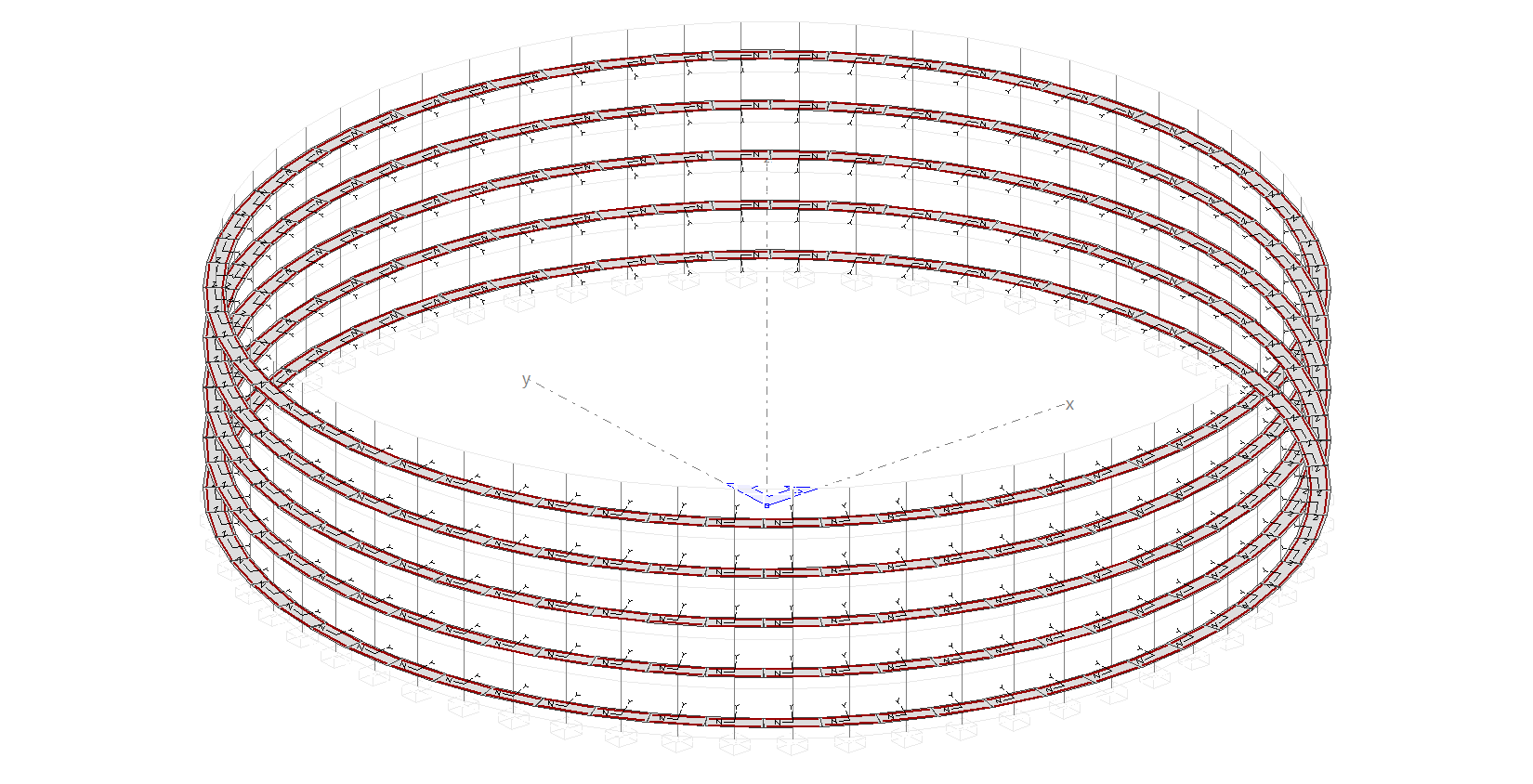
Nota: A la hora de crear las secciones, es muy importante pararse a pensar en los ejes. El plano de cada sección transversal es el YZ, ya que el X es el eje de la barra siempre. Al ser el eje Y de cada barra el que vamos a hacer que "apunte" hacia el origen, la sección la hemos hecho de 0.4 x 1.05 y no de 1.05 x 0.4. Si por error hacéis la sección con estas medidas, el depósito "no estaría cerrado". La experiencia nos lleva a sabernos esos trucos.
5) Introducción de los elementos horizontales.
En este apartado distinguiremos dos situaciones: depósito de hormigón armado y depósito con pretensado.
5.1.- Si tenemos un depósito de hormigón armado, los elementos horizontales serán "barras". Las secciones tendrán el mismo espesor que la de los elementos verticales, pero el ancho dependerá de si se sitúan en la base o cabeza del muro o si son intermedias. Puesto que tenemos un nudo a cada metro de altura, las secciones de la base y la cabeza serán de 0.5m de ancho (imagen inferior derecha), mientras que las intermedias serán de 1m (imagen inferior izquierda).
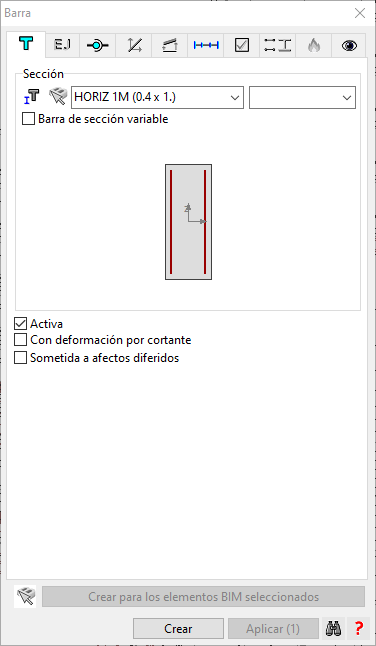
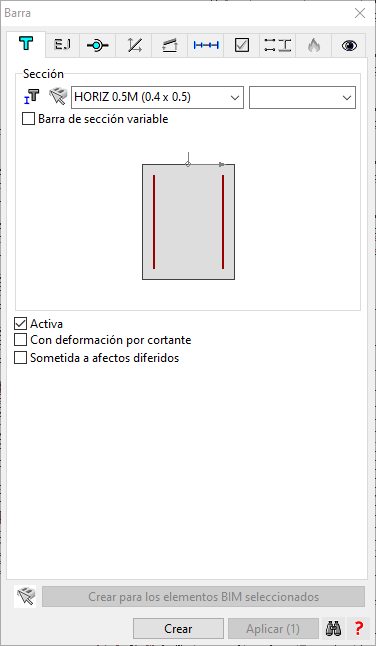
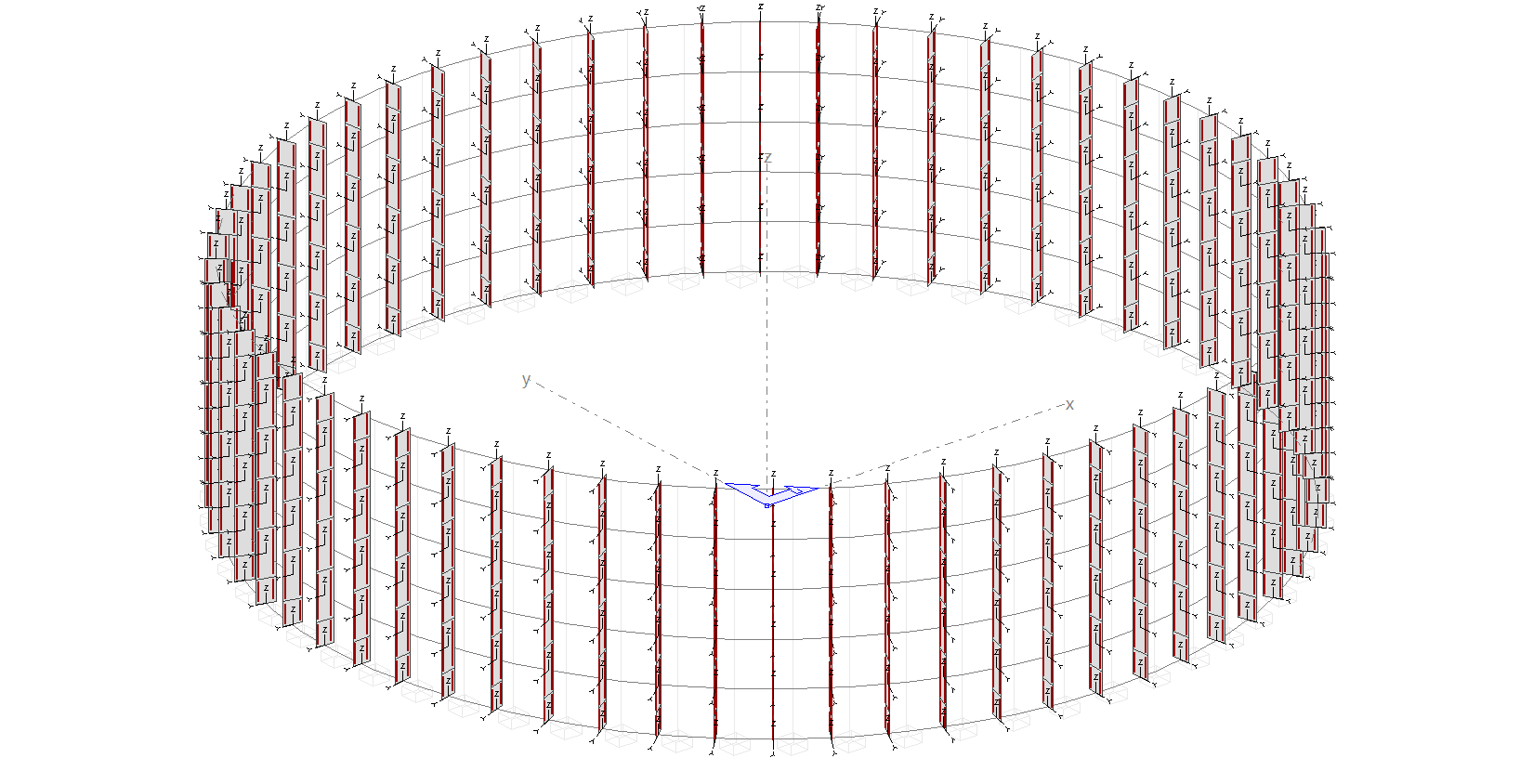
El emparrillado queda de la siguiente forma:
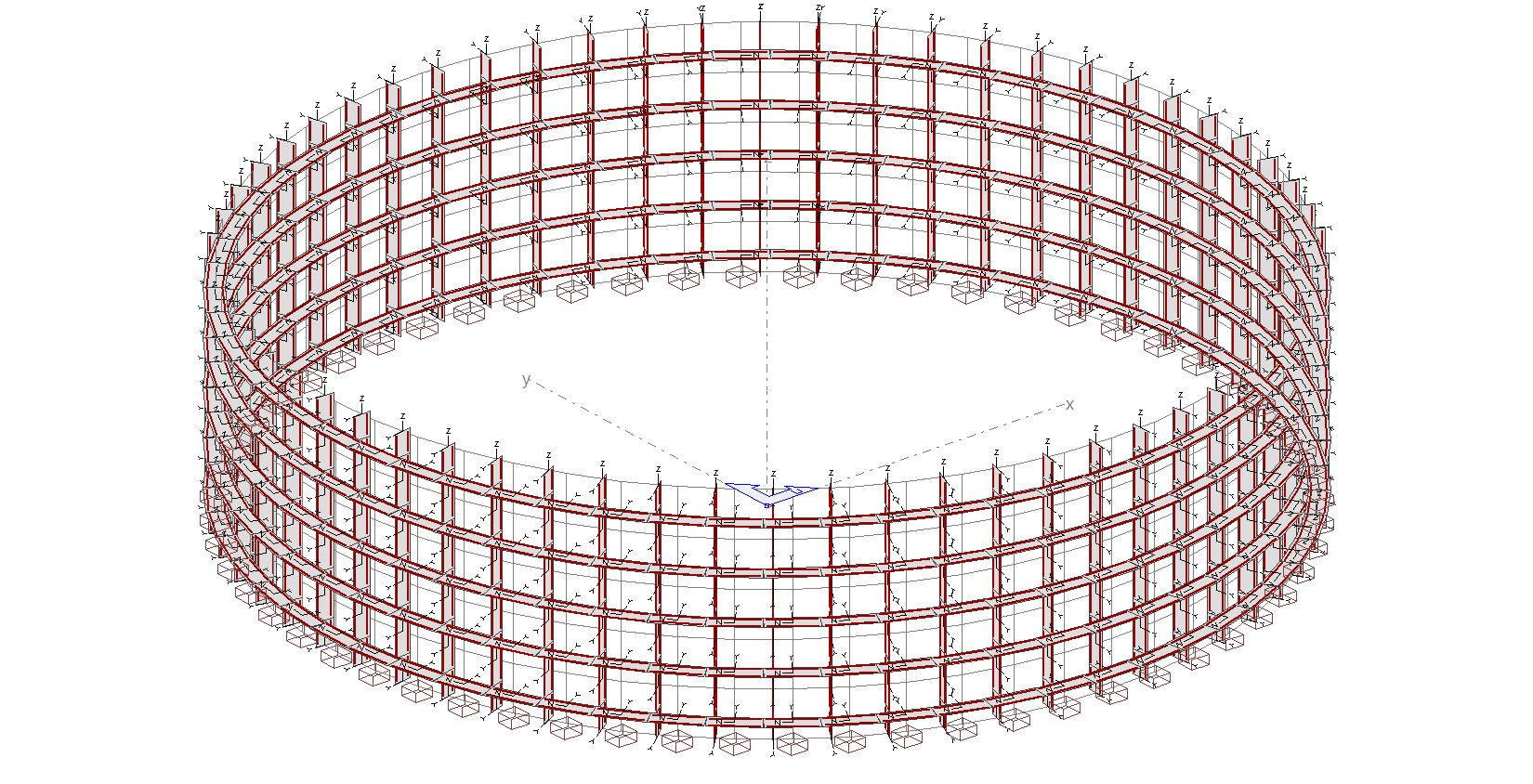
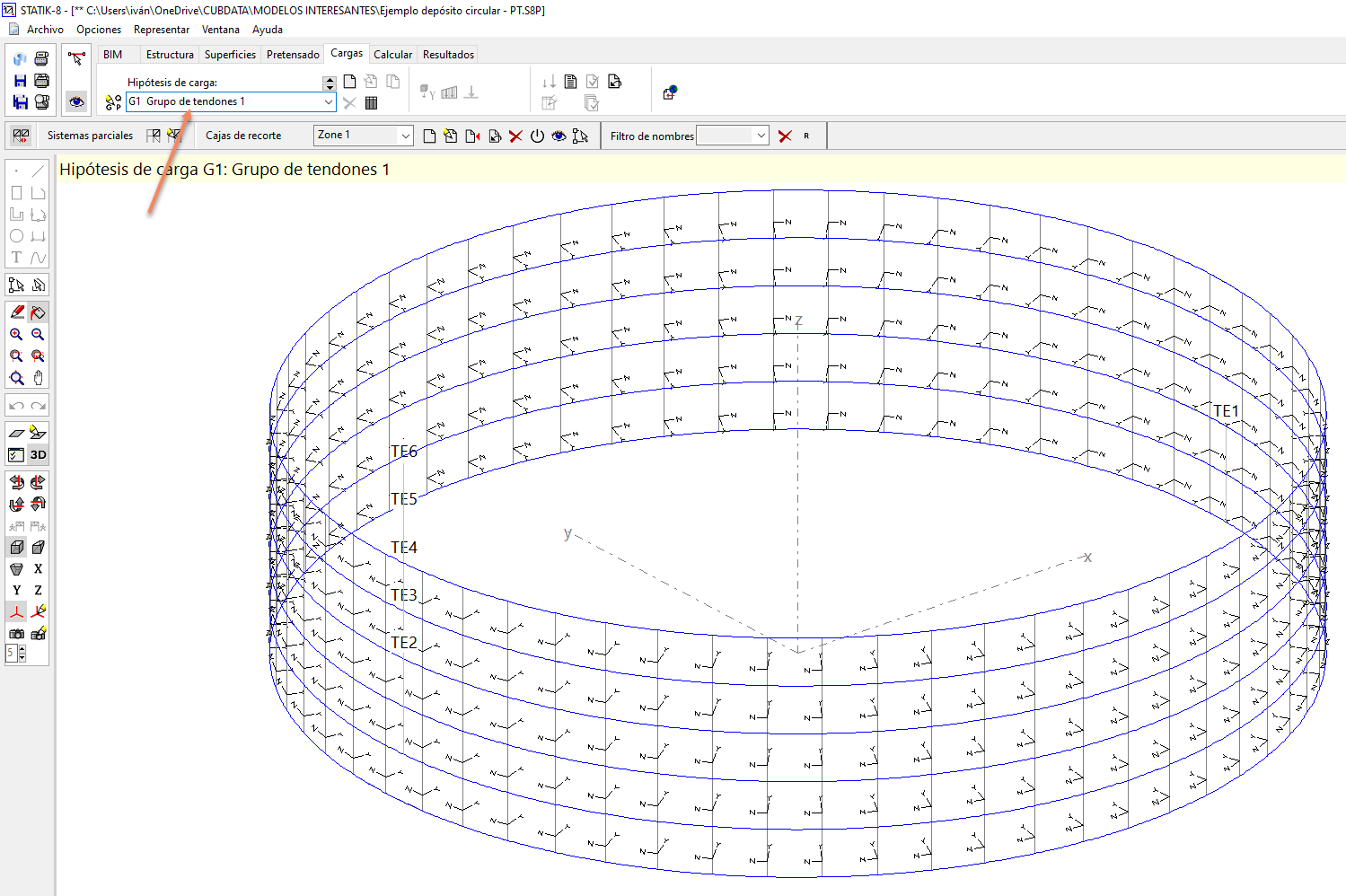
5.2.- Si tenemos que introducir tendones de pretensado, los elementos horizontales deberán introducirse mediante "líneas de estructura". En este caso, tendremos 6 anillos conformados por líneas de estructura (1 a cada metro de altura, incluyendo la cota 0) y tendrán las mismas secciones que las de las "barras" del apartado 5.1.
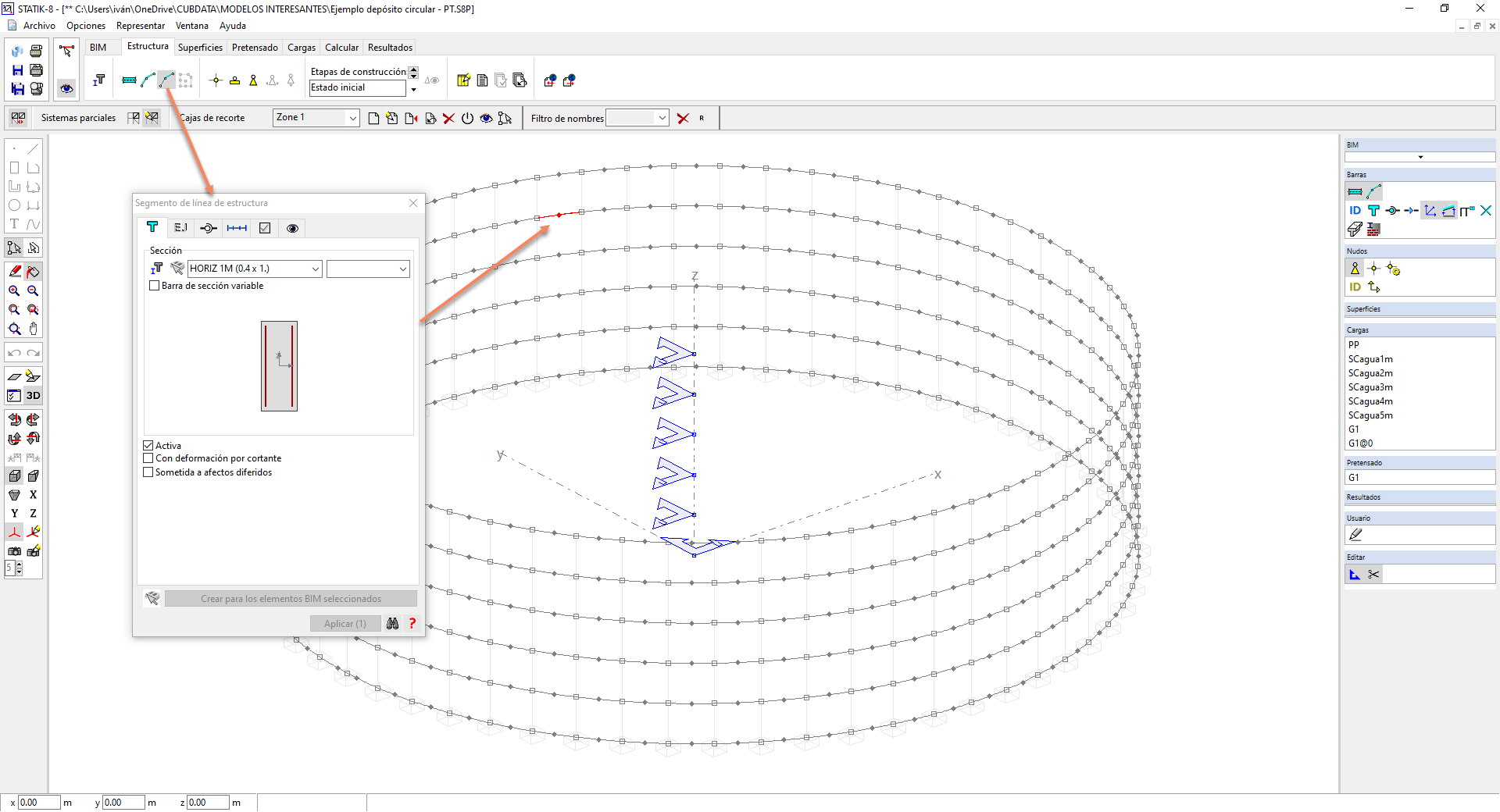
Puesto que los puntos de inicio y final de una línea de estructura no pueden coincidir, es necesario que introduzcamos 2 líneas de estructura por anillo:
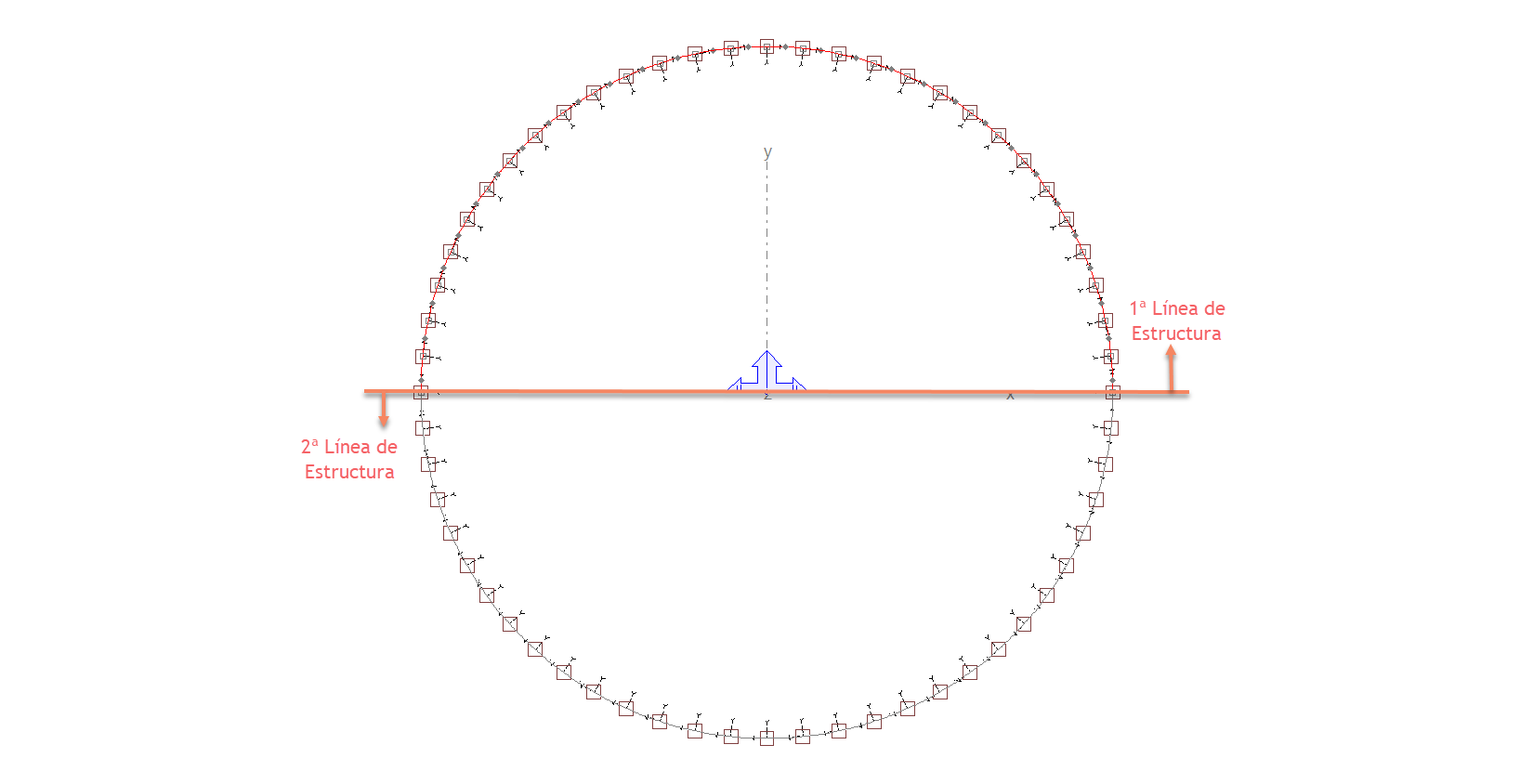
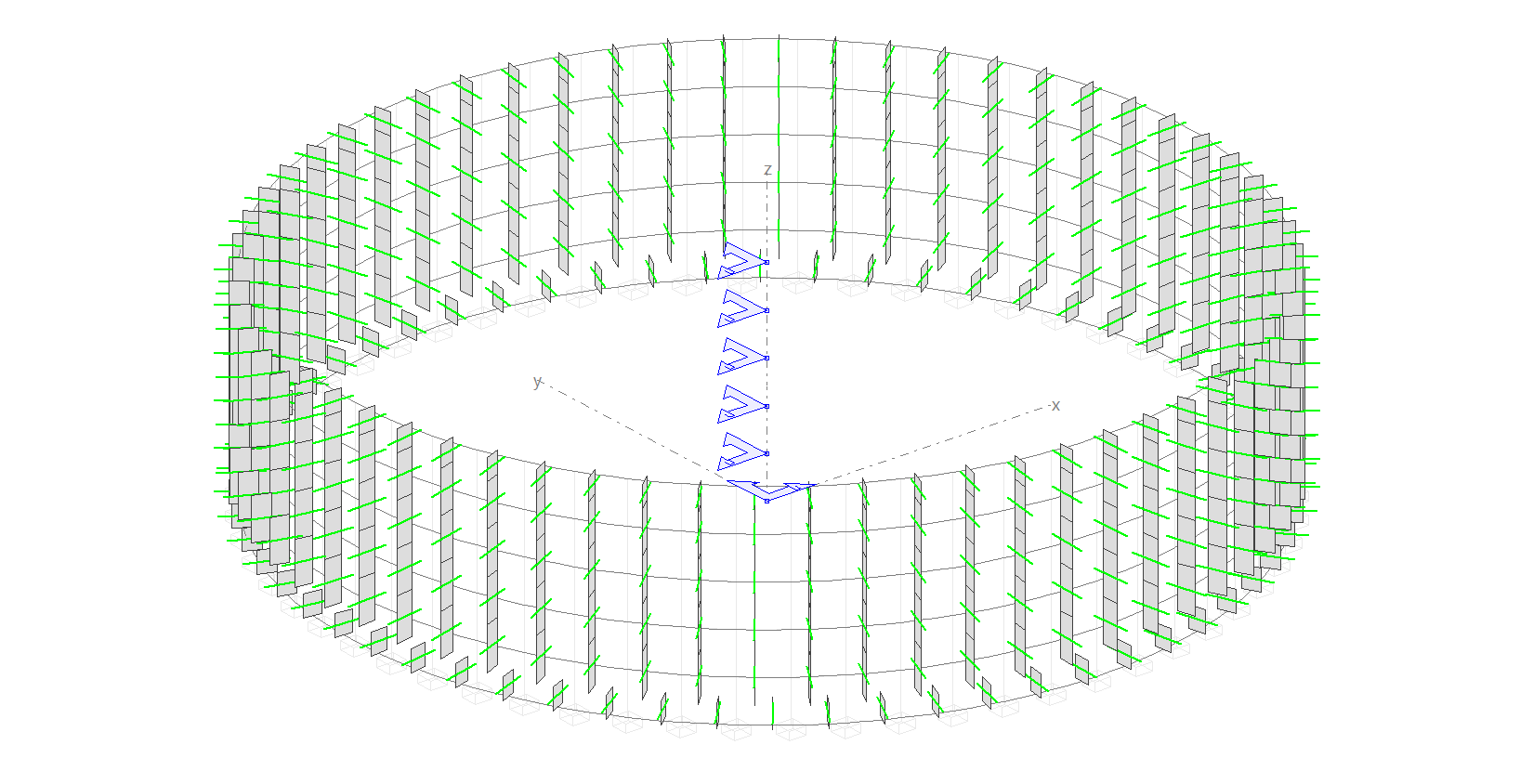
El emparrillado queda de la siguiente forma:
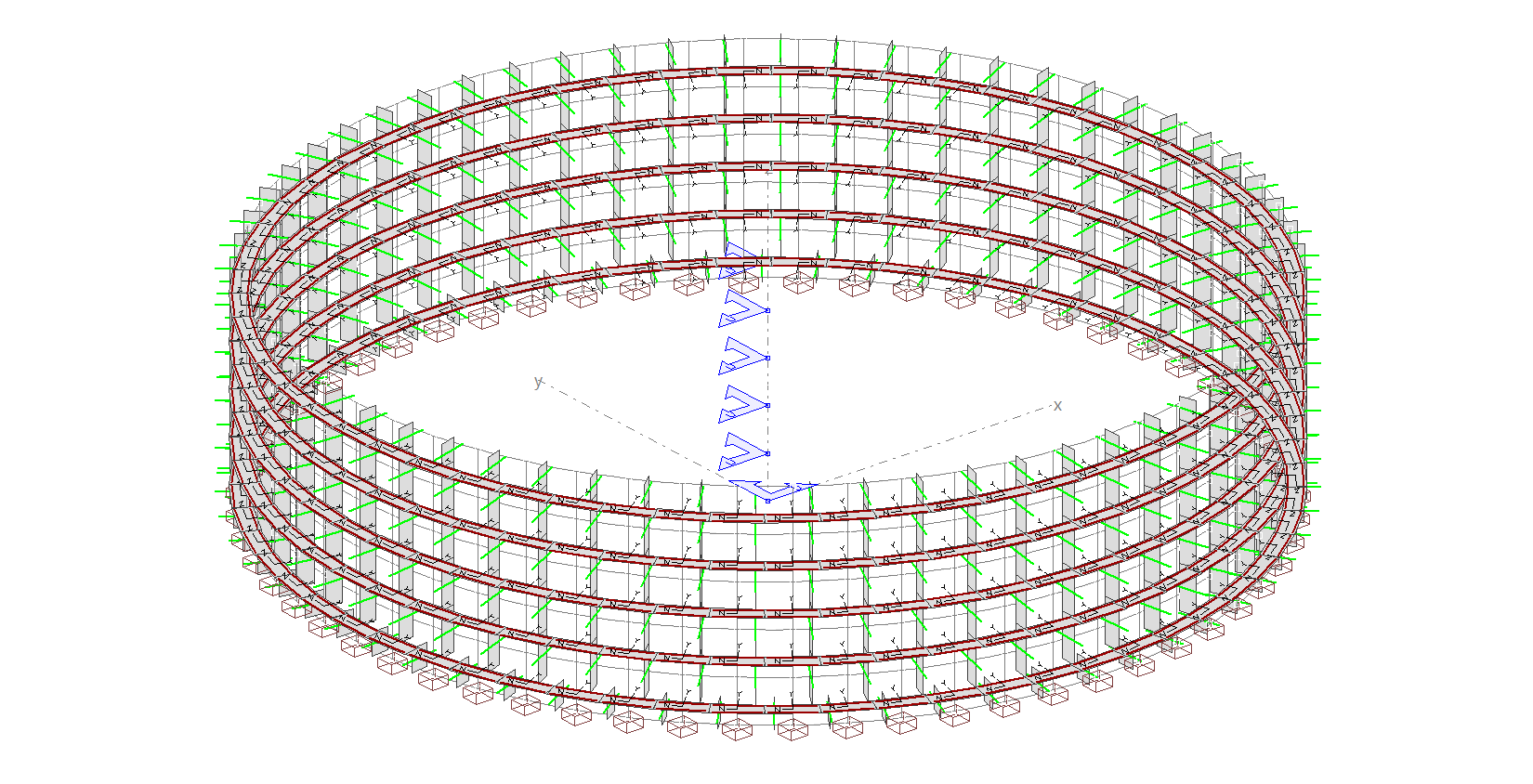
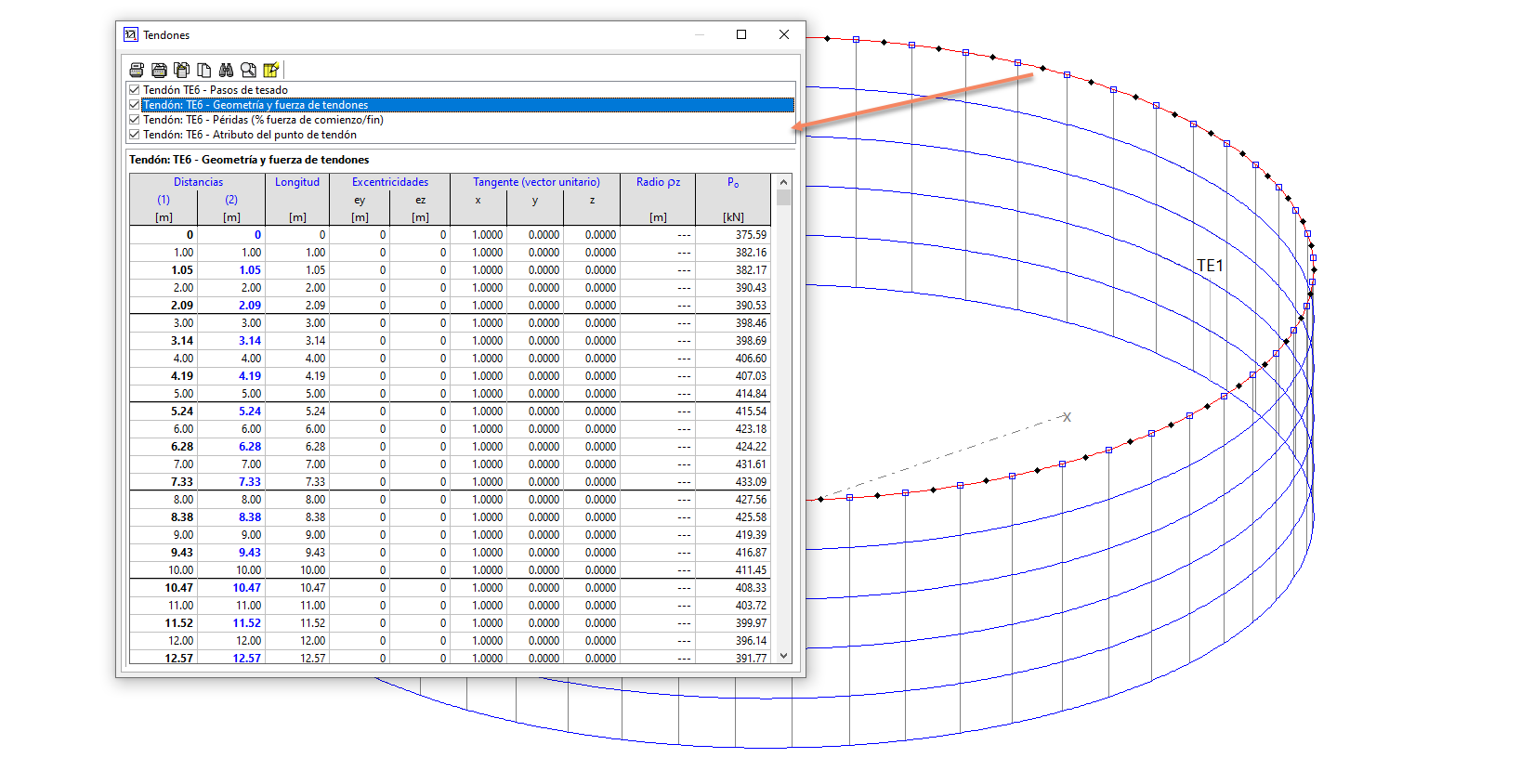
5.2.1.- En este caso, deberemos además introducir los tendones de pretensado. Esto lo haremos en la pestaña "Pretensado" de la siguiente forma:
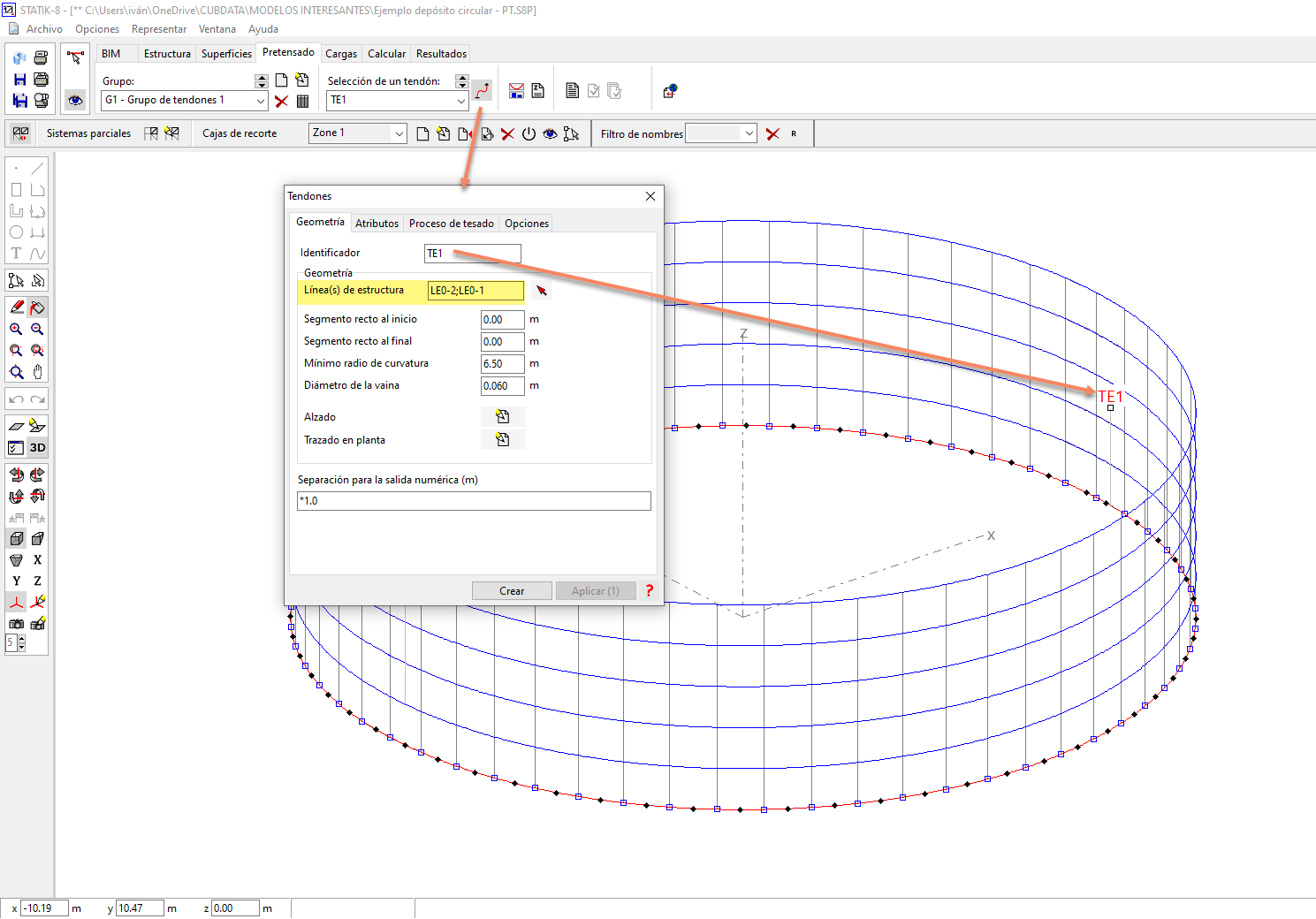
Es muy importante que nos fijemos en el campo destacado en amarillo en la figura superior. El tendón deberá estar a signado a las 2 líneas de estructura que conforman el anillo.
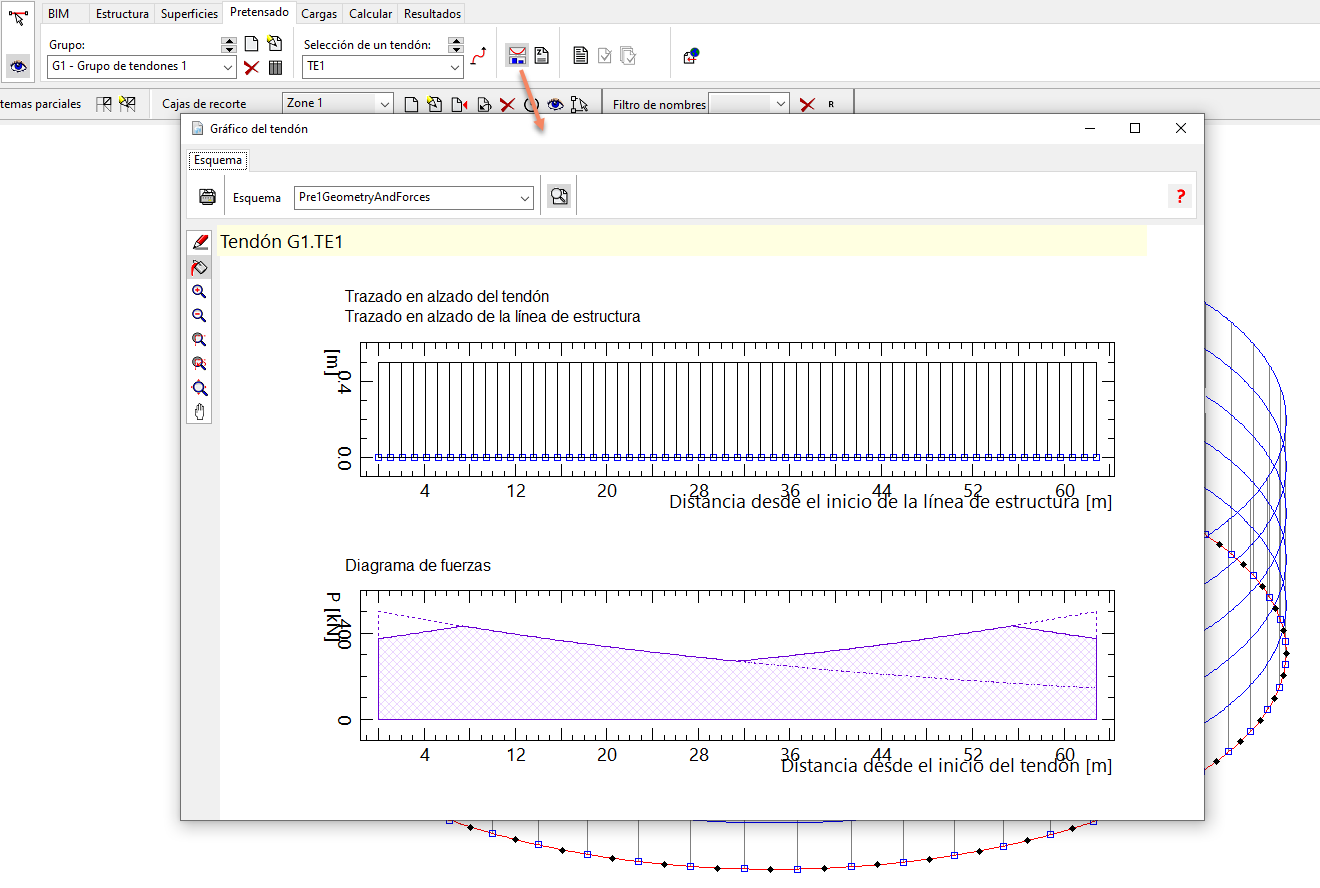
Una vez definamos todas las características de cada uno de los tendones (nº de cordones, proceso de tesado, etc.), podremos ver el gráfico de cada uno de ellos para verificar si todo es correcto.
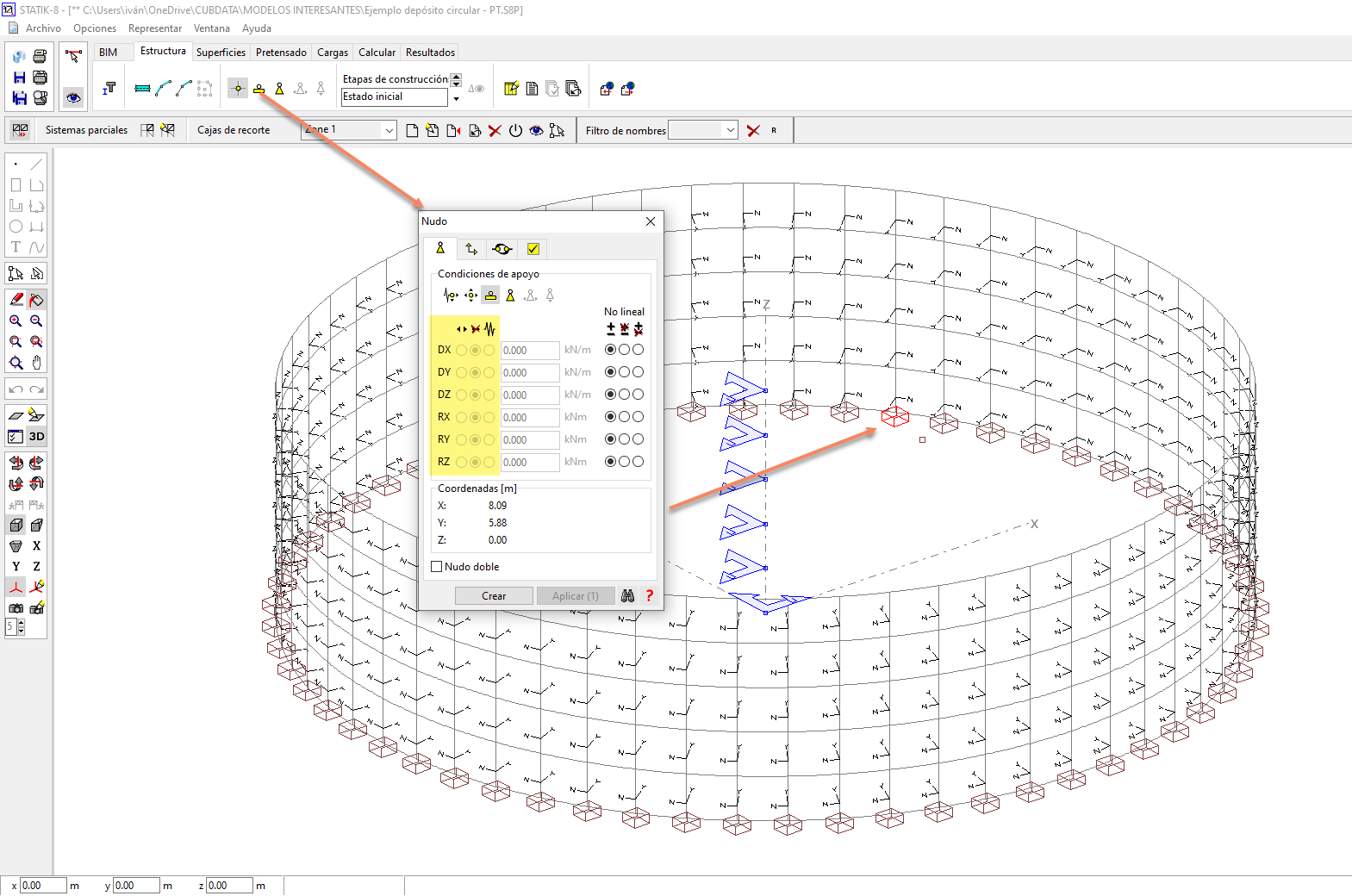
6) Definición de los apoyos. En este caso, como hemos comentado anteriormente, nuestro depósito estará empotrado en su base.
Cargas
- Presión hidrostática
La introducción de las cargas en un depósito sometido únicamente a la presión hidrostática del agua que contiene es muy sencilla.
Se trata de introducir una carga lineal en cada uno de los elementos verticales del muro que dependerá de la altura del agua y del ancho del segmento del muro considerado en la discretización.
En nuestro caso, tenemos una anchura del segmento de 1.05m, como hemos visto anteriormente. Si suponemos que el agua alcanza como máximo los 5m de altura que tiene el muro, la carga que debemos introducir en cada elemento es es:
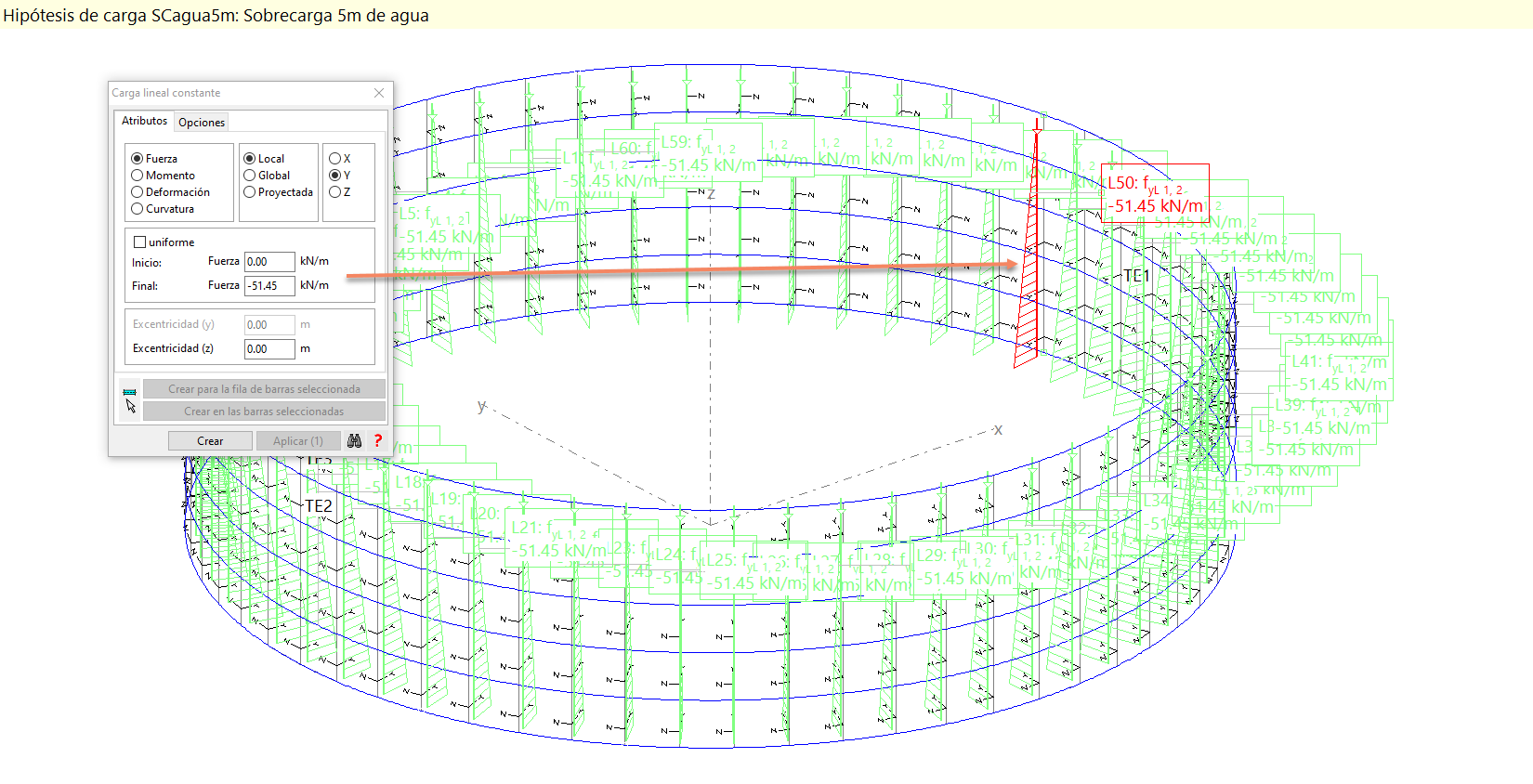
Donde el valor máximo de la distribución triangular en la base del depósito se calcula como:
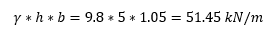
Para poder analizar el comportamiento del depósito cuando el agua está a 1, 2 ,3 y 4 metros, crearemos una hipótesis de carga para cada uno de estos casos del mismo modo que hemos hecho para la cota máxima. De este modo, podremos analizar también, por ejemplo, qué efecto genera el pretensado cuando el depósito está vacío.
- Pretensado
En el caso de que hayamos introducido tendones de pretensado, la carga correspondiente a cada uno de ellos será calculada automáticamente por STATIK:
AJUSTE DEL MODELO
Una vez hemos introducido el modelo es necesario hacer una serie de ajustes para que el comportamiento sea el deseado en base al criterio del ingeniero.
En este artículo vamos a dar una serie de consejos generales que se basan en la experiencia en el diseño de este tipo de estructuras aportada por diversas fuentes.
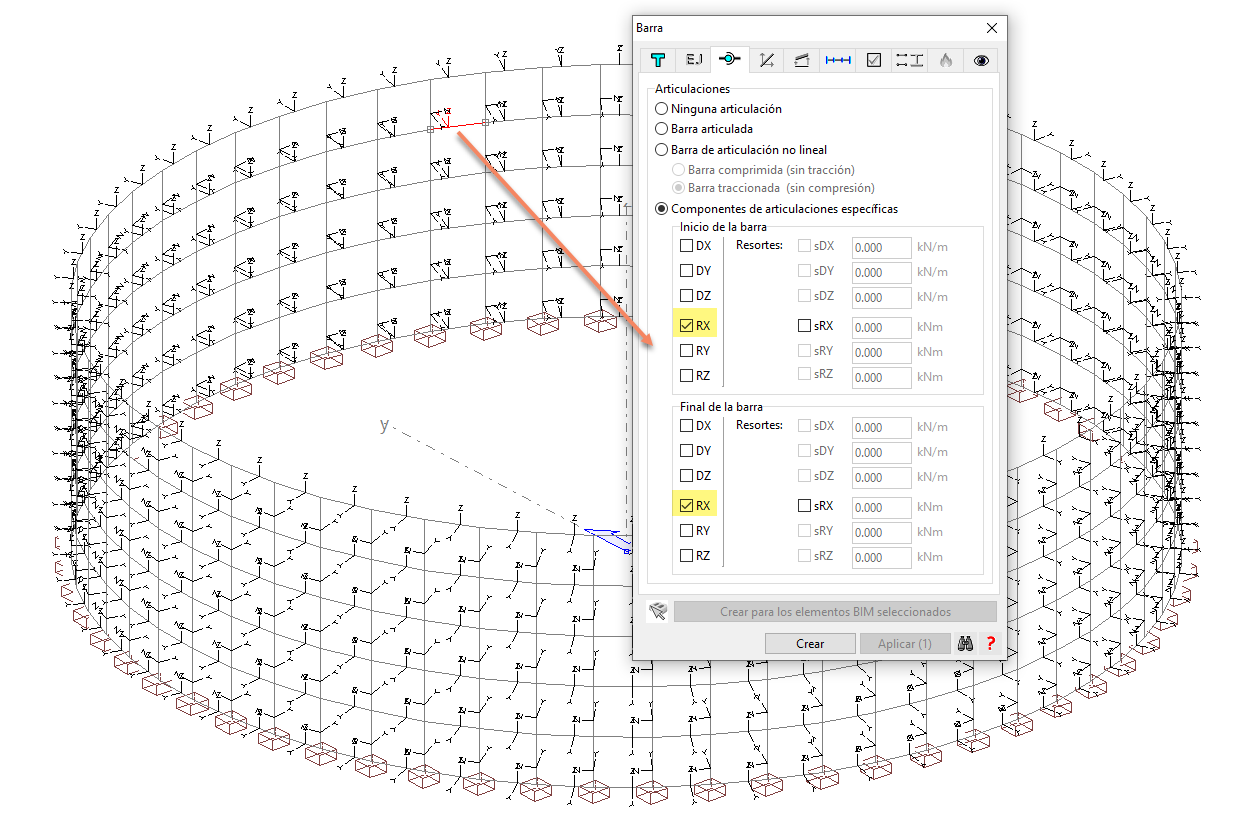
En primer lugar, indicar que, para evitar que los elementos horizontales introduzcan una coacción a la flexión de los elementos verticales, es conveniente liberar el giro alrededor de su eje longitudinal:
A continuación, vamos a hacer un número sencillo para comprobar el orden de magnitud de los valores obtenidos para los momentos y las deformaciones en los elementos verticales. Para un depósito empotrado en su base, las expresiones que proporcionan los momentos y las deformaciones en función de la altura cuando únicamente se somete a la presión hidrostática son:
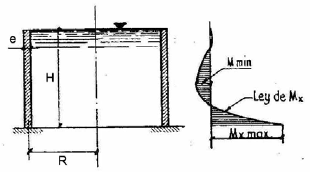
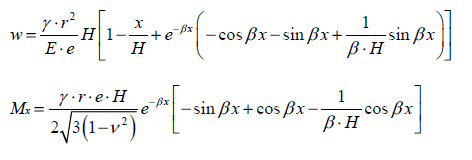
Introduciendo estas expresiones en una hoja de cálculo obtenemos los siguientes valores:
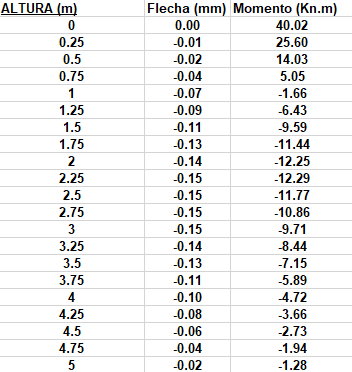
Que si los comparamos con lo obtenido en STATIK, fijándonos en el valor del momento en la base y en el máximo desplazamiento, por ejemplo:
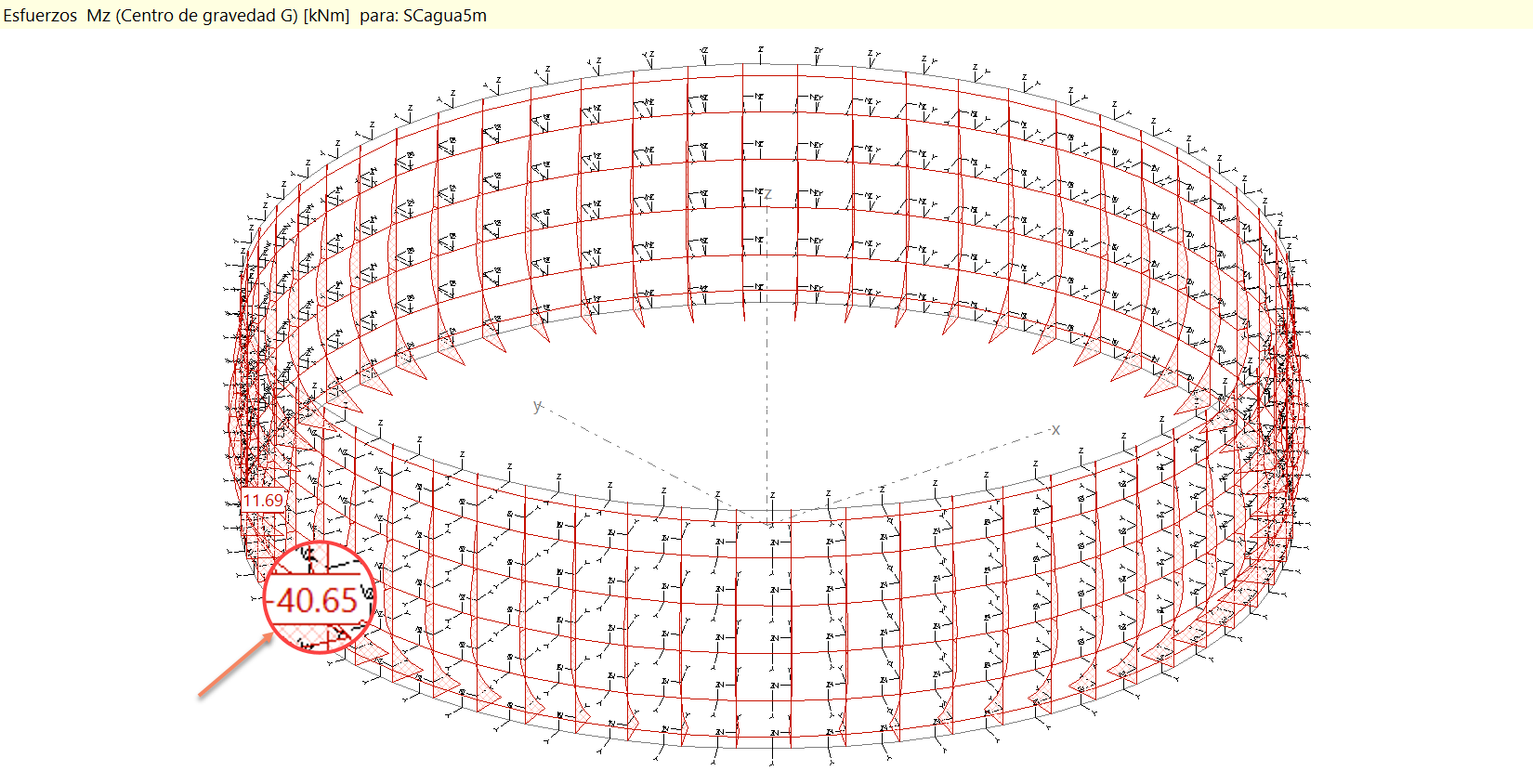
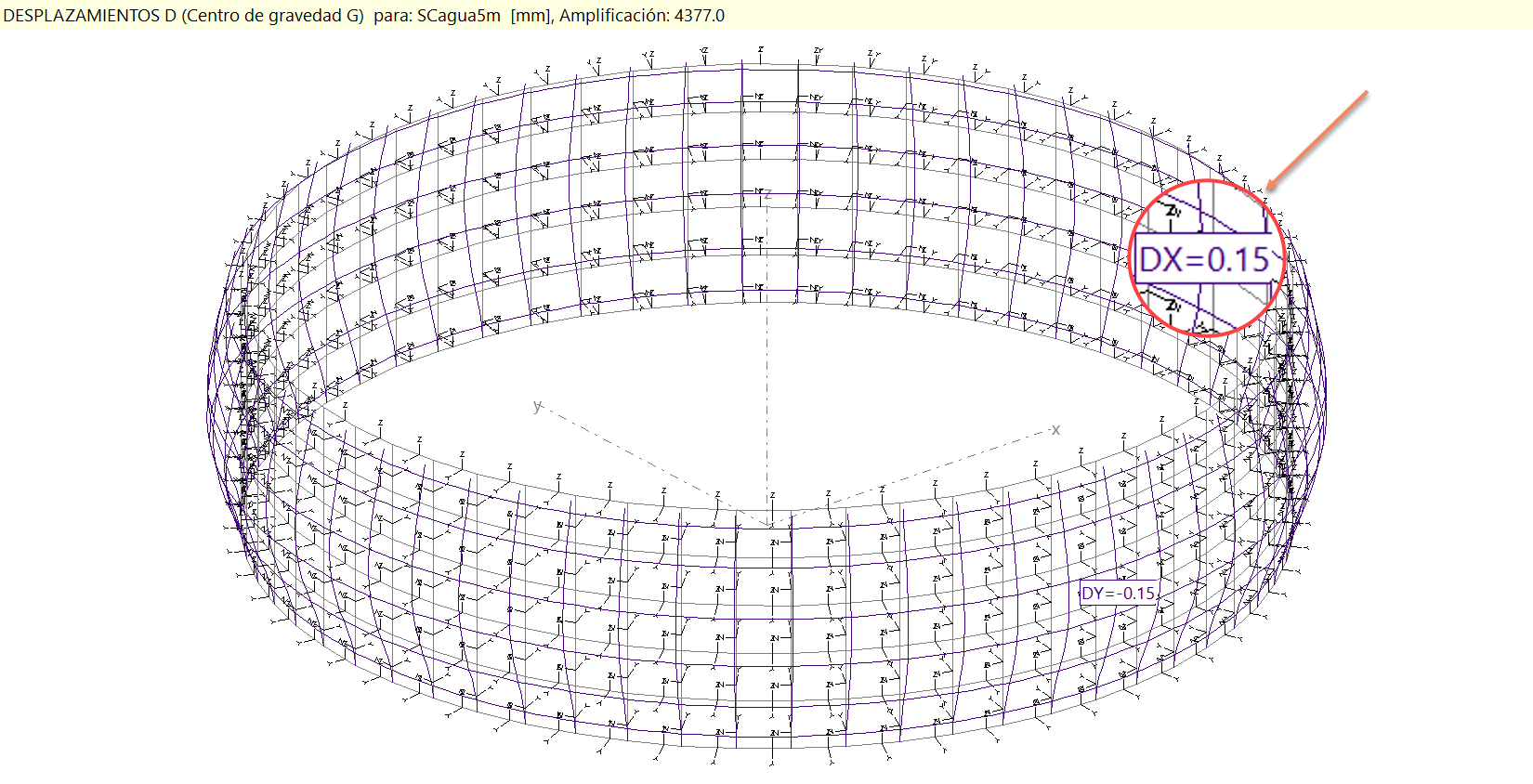
Vemos que el comportamiento del modelo se ajusta a la teoría.
En caso de tener pretensado, se deseará que los anillos estén siempre comprimidos, por lo que deberán ajustarse las fuerzas de tesado para que así sea, (teniendo en cuenta que el depósito pasará por unas etapas sin carga hidráulica - etapas de vacío - ).
COMENTARIOS ADICIONALES
En este artículo se ha desarrollado un ejemplo en el que no existe un gradiente térmico en las paredes del muro ni ninguna carga asimétrica que solicite a la estructura. Si tuviéramos alguna carga de esta naturaleza aparecerían momentos en los anillos que habría que considerar en el diseño.
Finalmente, indicar que, una vez desarrollado el modelo de barras de STATIK se podrá llevar a cabo el análisis y dimensionamiento completo de la armadura empleando la interacción directa con FAGUS. Esta herramienta permitirá, además, analizar en cada cara de los elementos y verificar la abertura de fisura.
Queremos dar las gracias a nuestros colegas griegos de de Cubus Hellas por sus comentarios en base a su basta experiencia en el dimensionamiento de depósitos circulares con STATIK (silos, cementeras, depuradoras...). Agradecer también a Jorge Calvo por su participación en los interesantes debates técnicos que surgen siempre a raíz de un artículo de estas características.
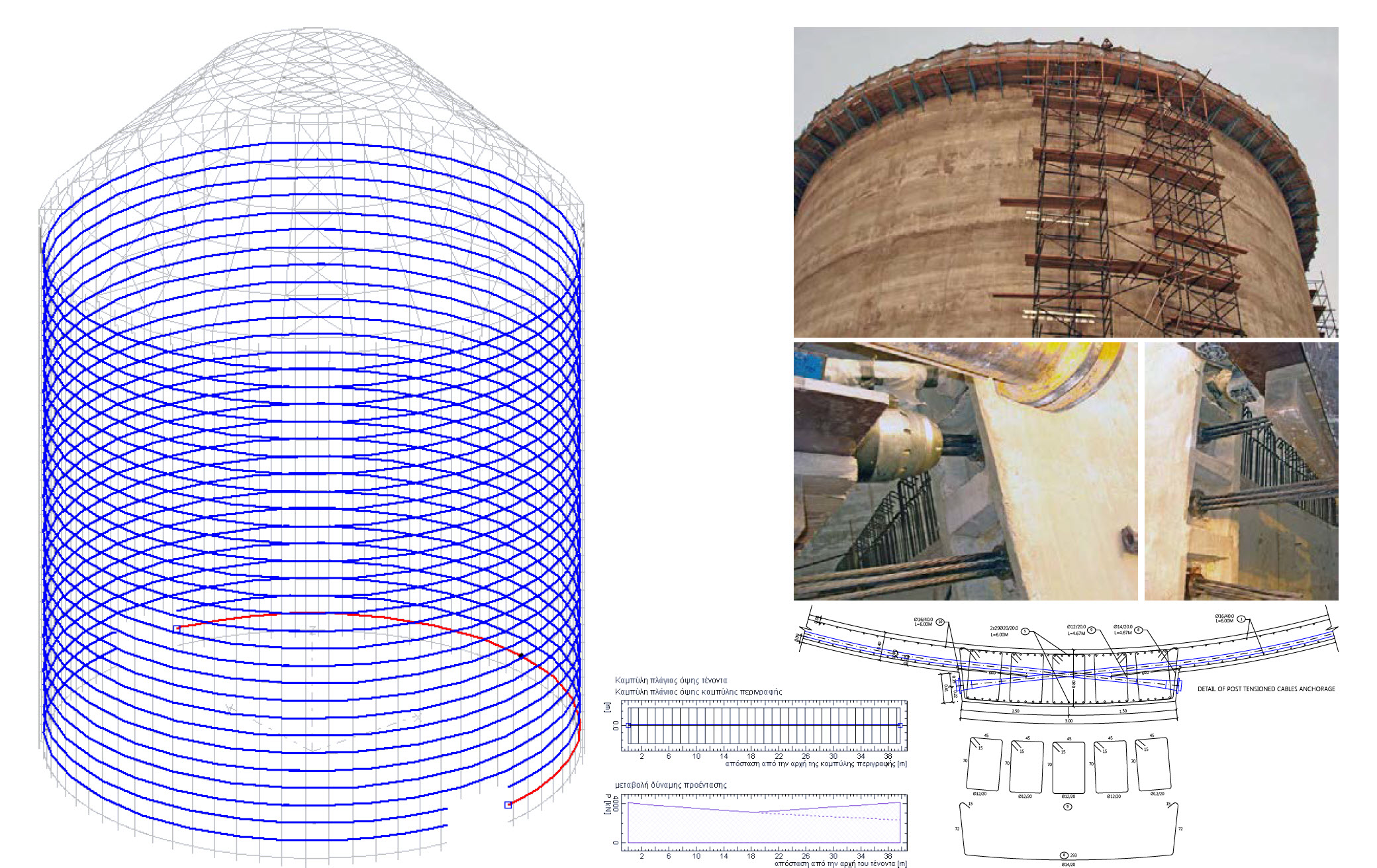

Ya hemos visto que diseñar este tipo de estructuras con STATIK es muy sencillo. ¿A qué esperas para hacerlo?
___
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado los únicos cursos online de FAGUS y CEDRUS avalados por CUBUS AG (licencia de estudiante disponible).

















