El objetivo de este artículo es explicar cómo FAGUS obtiene el momento de inercia torsional de sus secciones.
En primer lugar, haremos un pequeño resumen del modo en que el programa calcula el momento de inercia torsional según el tipo de sección que tengamos, particularizando después para el caso de secciones metálicas (perfiles estándar, secciones de pared delgada...).
En la página C-4 del manual de FAGUS, podemos ver la tabla siguiente, donde se especifica, de forma resumida, cómo se obtiene el momento de inercia torsional Ix según el tipo de sección:

Observaciones sobre cada uno de los modelos presentados en la tabla anterior
- MODELOS Nº1 Y Nº2: SECCIONES MACIZAS RECTANGULARES O CIRCULARES
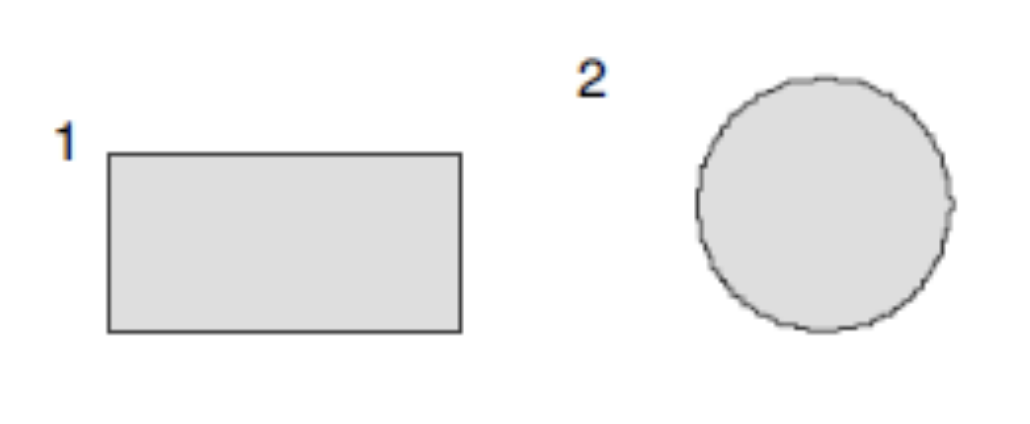
La relación entre el momento de torsión y la derivada de la rotación del elemento alrededor de su eje longitudinal se define como:
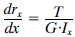
En este caso, Ix denota el momento de inercia torsional, resistencia torsional o resistencia al pandeo. Las secciones armadas de pequeñas dimensiones son generalmente macizas y el módulo de torsión se calcula en base a la teoría de St. Venant (analogía de la membrana). Para secciones compactas genéricas, en general el valor exacto únicamente puede ser obtenido resolviendo la ecuación diferencial (utilizando un programa de Elementos Finitos). FAGUS, como veremos a lo largo de este artículo, dispone de esta herramienta.
- MODELO Nº3: SECCIONES DE PARED DELGADA
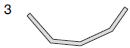
Para subsecciones poligonales que presenten un gran perímetro (en relación al área), "l" y "t" pueden ser estimadas por el programa a partir de esos dos valores. De todos modos, en el caso de estar trabajando con una sección de pared delgada, siempre es mejor trabajar introduciendo los elementos que la constituyan con sus dimensiones.
- MODELO Nº4: SECCIONES MACIZAS DE FORMA GENÉRICA
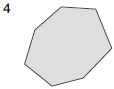
El radio r se obtiene para un círculo con un área equivalente a la de la sección que tengamos.
- MODELO Nº5: PERFILES METÁLICOS ESTÁNDAR
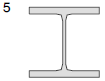
El momento de inercia torsional Ix será obtenido a partir de datos tomados del prontuario.
- MODELOS Nº6 Y Nº7: SECCIONES POLIGONALES GENÉRICAS
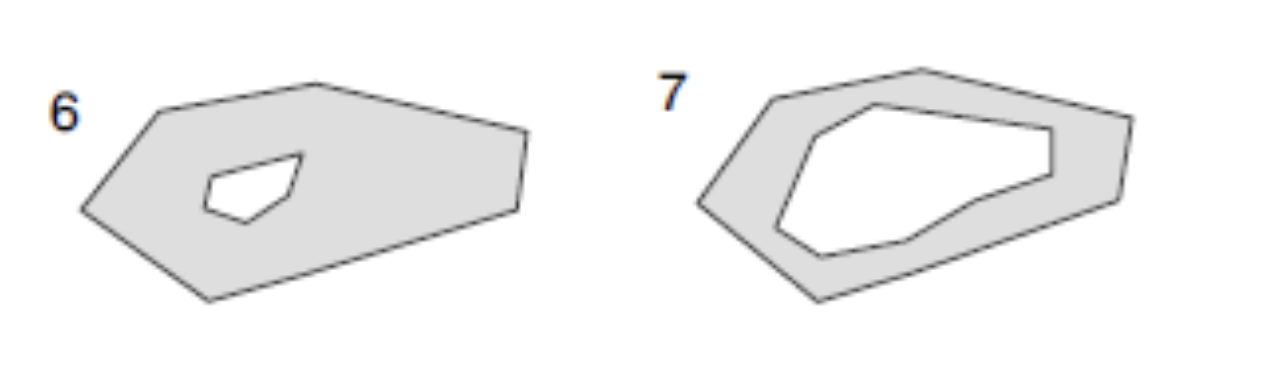

Para secciones poligonales genéricas y sin información adicional, el programa asignará automáticamente cada una de las subsecciones a uno de los casos presentados arriba. En consecuencia, las dimensiones necesarias en las fórmulas presentadas serán estimadas a partir del área y de la longitud del contorno. El valor de Ix obtenido por FAGUS debe ser comprobado y remplazado, si fuera necesario, por una valor proporcionado por el usuario, especialmente si el valor del momento de inercia torsional influye de forma determinante en el resto de análisis.
Para una sección compuesta por varias subsecciones, las partes de las subsecciones son determinadas individualmente y sumadas al final. Únicamente las partes de la sección creadas con contornos contribuyen al valor de Ix (por ejemplo, las armaduras no).
Para secciones con huecos grandes, el momento de inercia torsional se calcula a partir de la fórmula de Bredt:
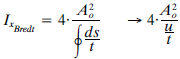
donde:
A0: área encerrada de la sección cajón equivalente.
u: perímetro del área encerrada.
t: (se asume como constante) espesor de la pared de la sección cajón equivalente.
Los parámetros A0 y u son estimados por el programa a partir de las áreas individuales de los lados del polígono y de la longitud del contorno.
El modelo empleado se especifica en la salida de resultados tabular para cada una de las subsecciones.
- MODELOS Nº8 Y Nº9: SECCIONES DE PARED DELGADA
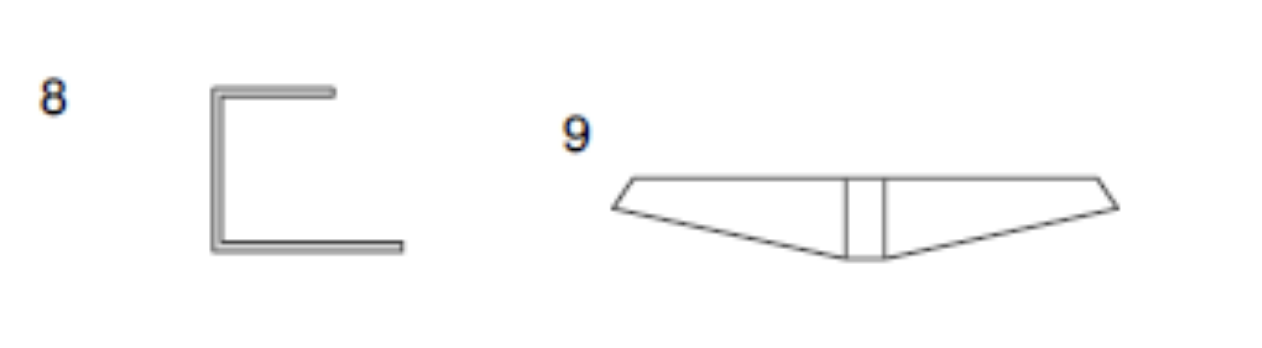

El momento de inercia torsional de St. Venant para secciones de pared delgada abiertas se obtiene como el sumatorio de los elementos pared que la componen. Si los elementos pared componen una sección cerrada con uno o más huecos, el módulo de torsión se obtiene básicamente a partir de la fórmula de Bredt para la "circunferencia externa". Una sección formada por elementos de pared delgada proporciona valores correctos de Ix, por lo que, si se desea obtener el valor exacto del módulo de torsión de una viga cajón de un puente compuesta por varias células, se recomienda modelizarla también mediante elementos de pared delgada.
Obtención del momento de inercia torsional lx mediante un análisis de elementos finitos
Para secciones formadas a partir de un contorno definido por un polígono (con la posible inclusión de huecos), el momento de inercia torsional de acuerdo con la teoría de St. Venant puede obtenerse a partir de un análisis de elementos finitos. Esta opción puede seleccionarse en la pestaña "Variantes">"Propiedades de la Variante">"Valores de la sección".
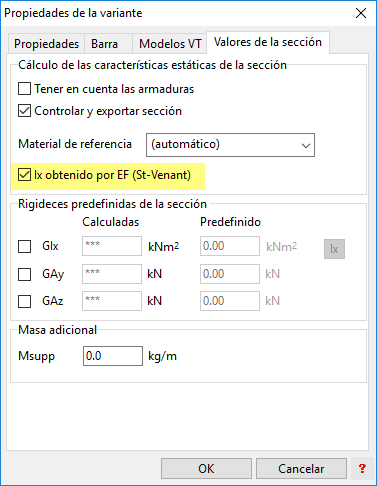
El cálculo numérico se basa en la teoría presentada a continuación:
Con la introducción de una función de tensiones Φ, el comportamiento elástico a torsión de una región homogénea se describe mediante la siguiente ecuación:
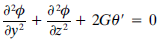
donde:
Θ: ángulo de rotación por unidad de longitud
G: módulo de cortante
con las siguientes condiciones de contorno:
Borde exterior: Φ=0
Huecos: Φ=constante a lo largo del hueco
Con la ayuda de la función de tensiones Φ, las componentes de la tensión de corte pueden ser especificadas en cualquier punto:
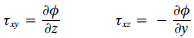
El cambio de variable es:
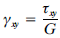
El momento de inercia torsional resulta de la integración sobre el área total de la sección:
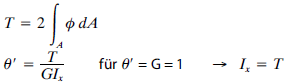
Considerando todo lo explicado, vamos a particularizar para el caso de secciones formadas por perfiles estándar, para terminar concluyendo con algunas recomendaciones sobre cómo obtener el momento de inercia torsional en el caso de un perfil metálico estándar y en el caso de una sección en cajón compuesta por dos perfiles estándar.
Estudio del caso de perfiles metálicos
1.- PERFIL ESTÁNDAR
Si tomamos, por ejemplo, un perfil HEB200:
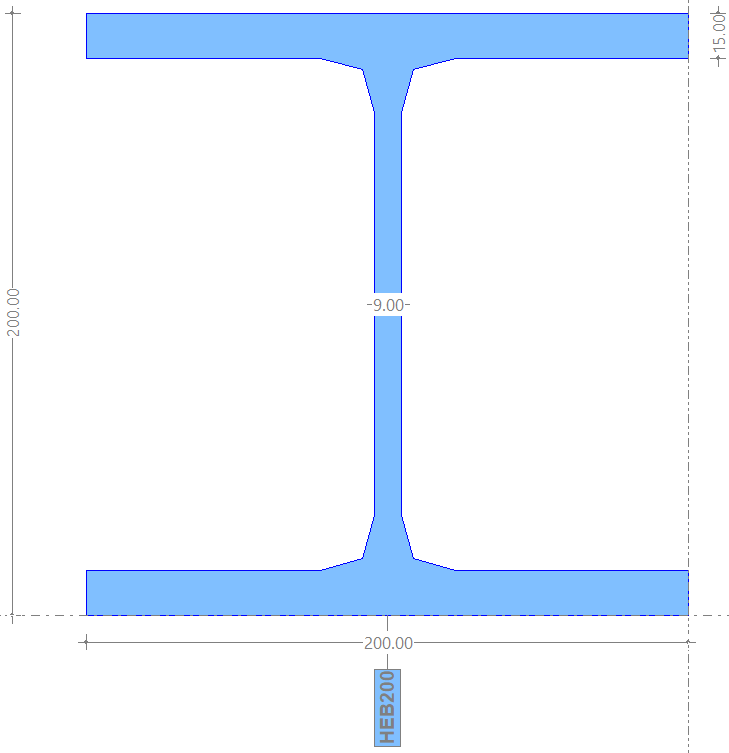
Podemos observar, en cualquier prontuario, que su momento de inercia torsional es:
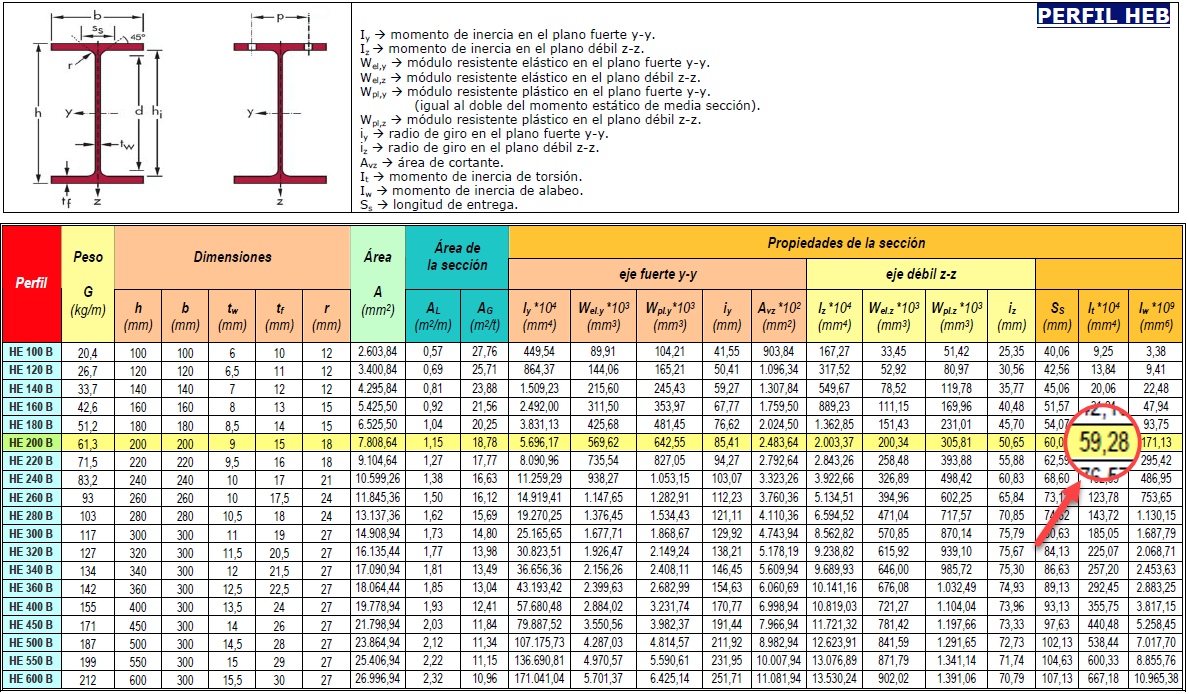
Ix = 59.28 cm4
Si comparamos este valor con el que proporciona FAGUS:
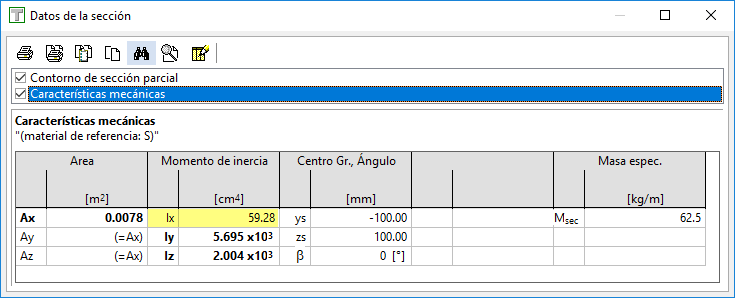
Vemos que, efectivamente, el programa está tomando este valor directamente de la tabla.
Si seleccionamos la opción del cálculo por St. Venant:
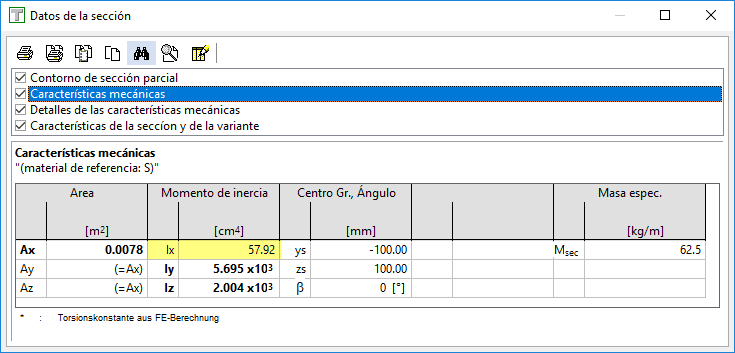
Vemos que el valor ya no se corresponde con el anterior, sino que el programa lo está obteniendo de acuerdo con el cálculo numérico presentado arriba.
2.- SECCIÓN CAJÓN FORMADA POR 2xHEB200
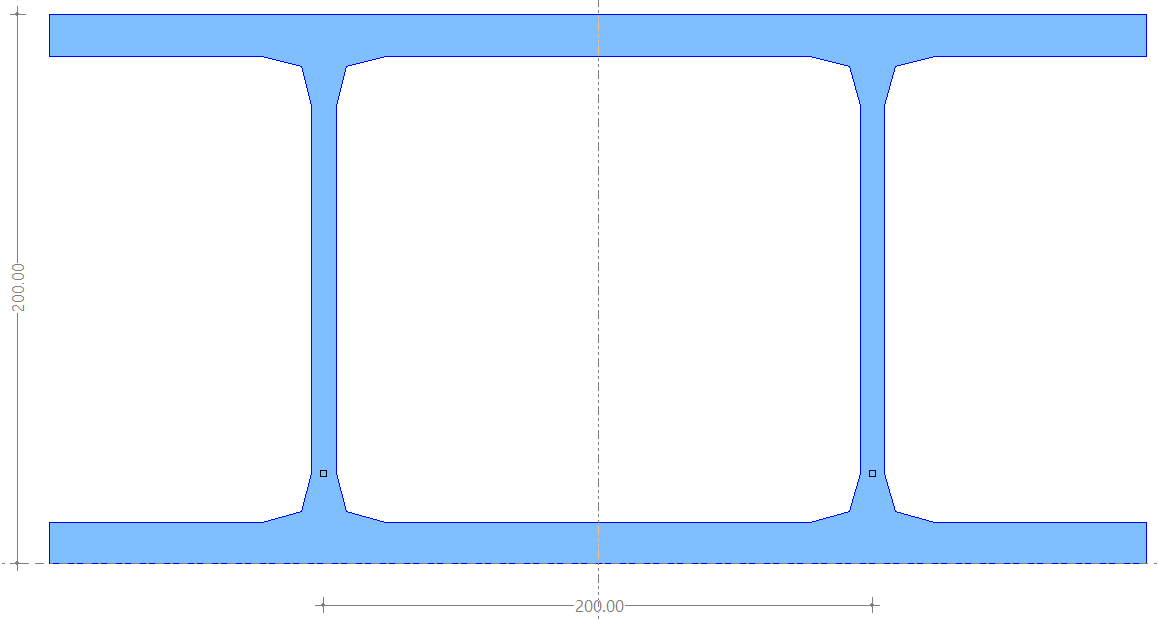
en este caso obtendremos el valor de Ix según 4 modelos diferentes:
2.a) Sección introducida como polígono cerrado + hueco -> Ix por fórmula de Bredt
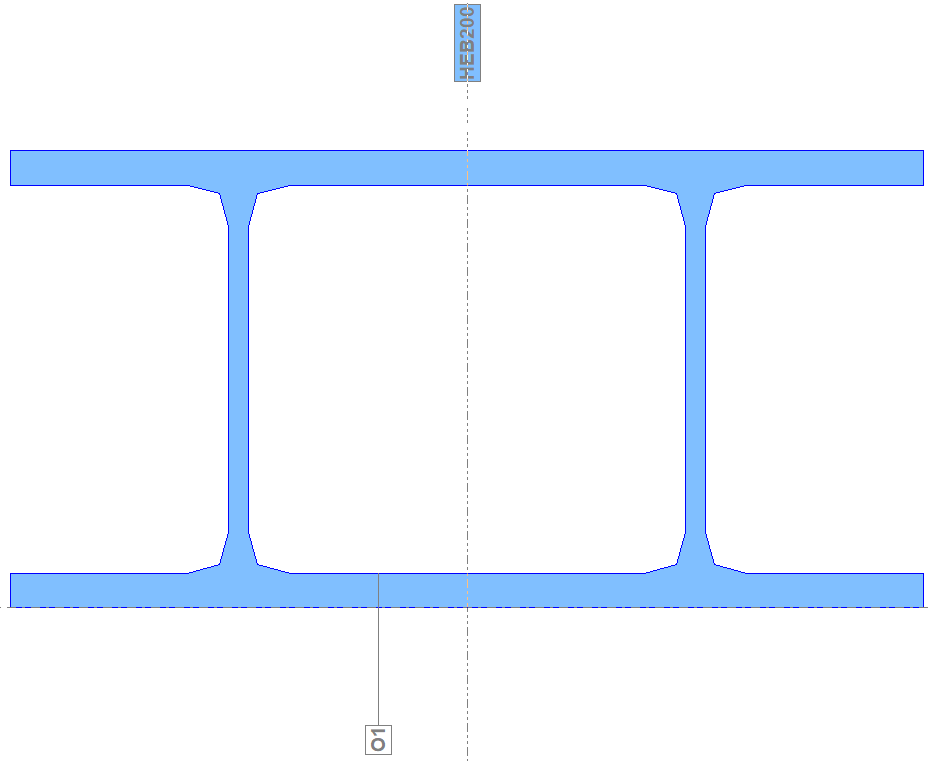
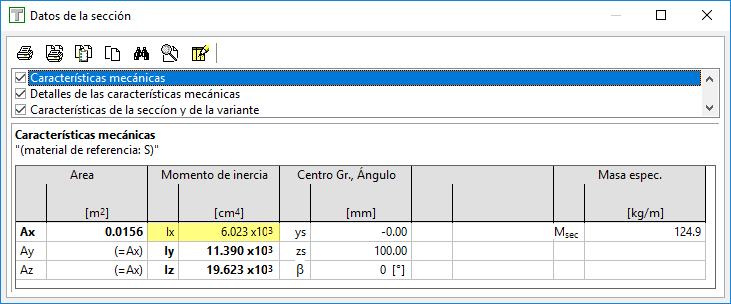
Ix = 6023 cm4
En la tabla siguiente vemos como, según lo explicado arriba, el valor se obtiene a partir de los valores de área y perímetro:
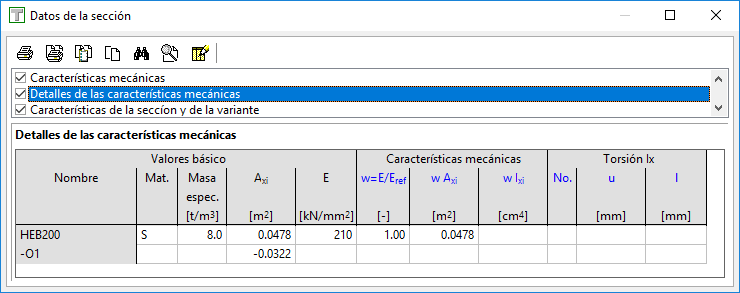
2.b) Sección introducida como polígono cerrado + hueco -> Ix por St. Venant
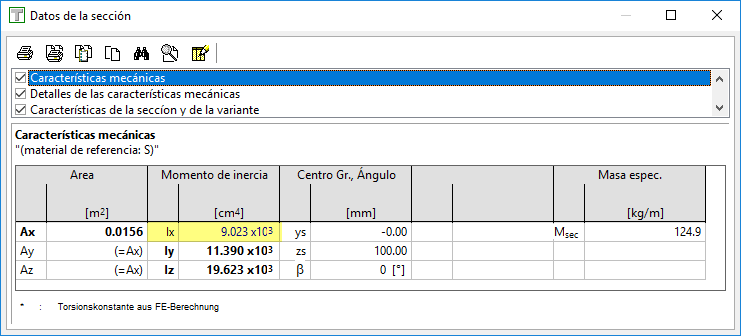
Ix = 9023 cm4
En la tabla siguiente vemos como, según lo explicado arriba, el valor se obtiene numéricamente por elementos finitos y no a partir de los valores de área y perímetro:
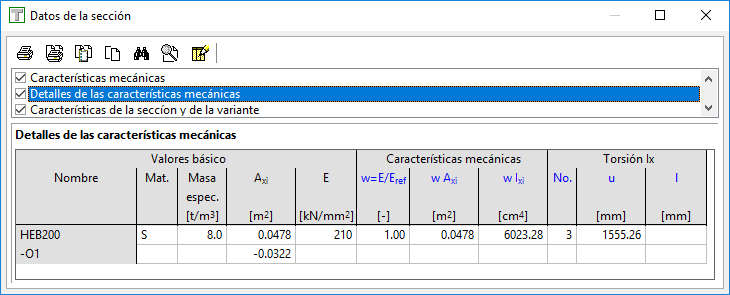
2.c) Sección introducida con pared delgada -> Ix por fórmula de Bredt
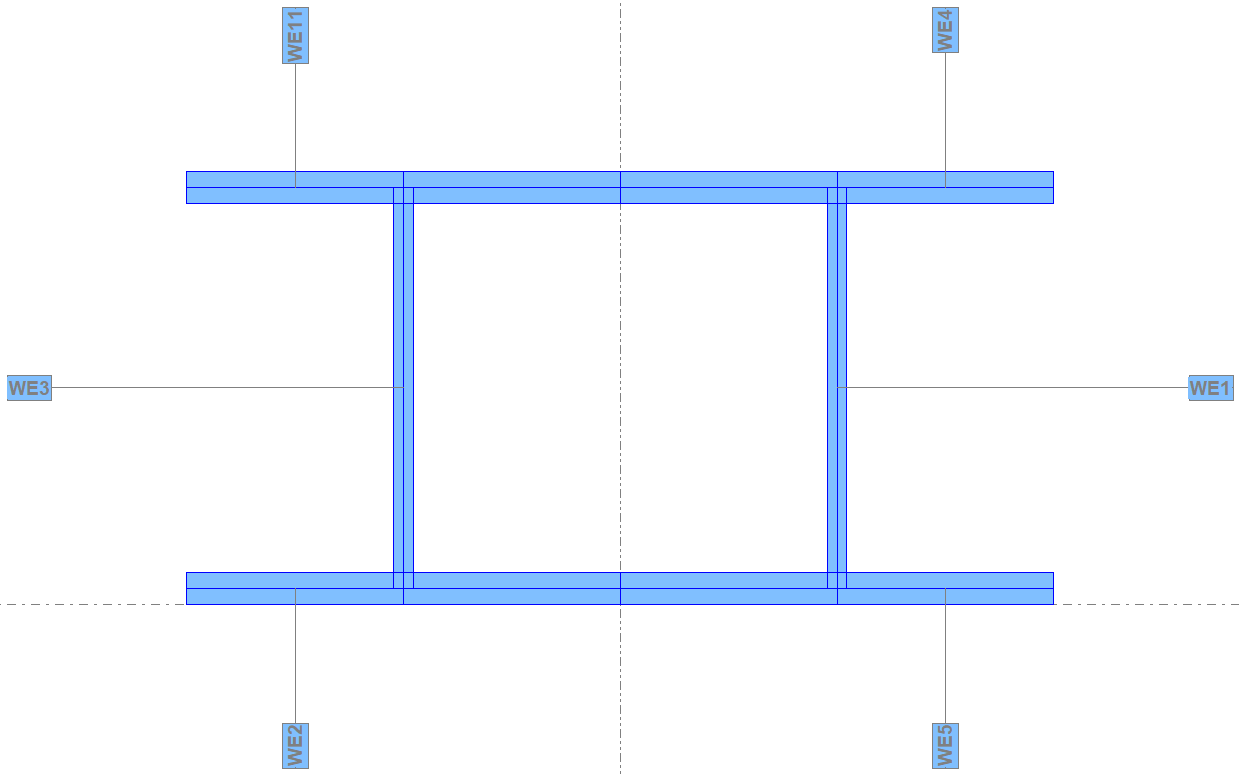
Para secciones de pared delgada cerradas como la presentada (o con más de una célula, si fuera el caso), el momento de inercia torsional para cada célula o hueco se calcula mediante la fórmula de Bredt:
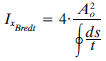
Para múltiples células, el momento de inercia torsional y el flujo de cortantes se dan por condiciones de compatibilidad y equilibrio. Esto lo lleva a cabo FAGUS automáticamente resolviendo el correspondiente sistema de ecuaciones.
Para el caso concreto del valor de Ix de la sección, el valor que se da por defecto es la suma de las dos siguientes partes:
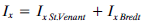
En el caso de secciones de pared delgada, el primer término puede despreciarse. La parte de Bredt que determina el programa depende de si existen uno o más huecos cerrados (células) (conexión materializada uniendo los puntos extremos de cada elemento). La topología reconocida por el programa puede verificarse en la salida de resultados tabular. En este caso:
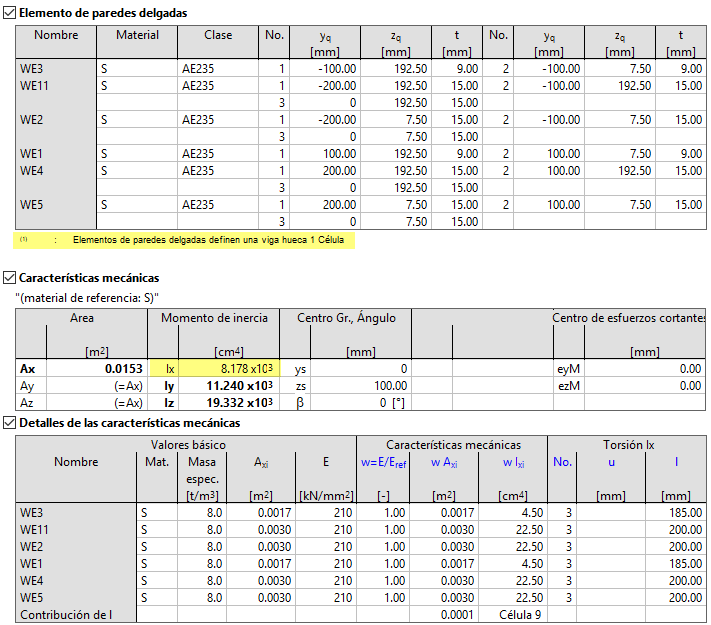
Vemos que se obtiene un momento de inercia torsional Ix = 8178 cm4, valor que podemos comparar con el obtenido manualmente y de forma aproximada procediendo del modo habitual:
A0 = (h-tf)(b/2-tw) = (20-1.5)(40/2-0.9) = 353.35 cm2
u = [(h-tf)+(b/2-tw)]2 = [(20-1.5)+(40/2-0.9)]2 = 75.2 cm2
Ix = [4353.35^2(1.5+0.9)/2]/75.2 = 7969.55 cm4
Como vemos, llegamos a un valor muy similar al proporcionado por FAGUS (el cálculo manual se trata de una aproximación).
2.d) Sección introducida con pared delgada -> Ix por St. Venant
Seleccionando esta opción deberíamos obtener el mismo valor que en el caso c) de acuerdo con los explicado en relación a la no consideración del término de St. Venant en la fórmula:
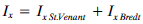
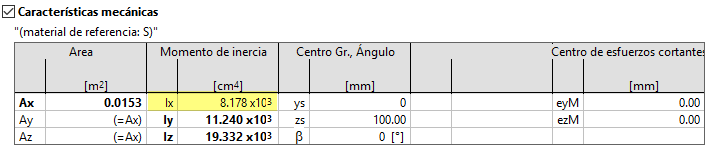
En la tabla anterior vemos que, efectivamente, así es.
CONCLUSIONES
Cuando nuestra sección esté compuesta de un único perfil estándar, introduciremos la sección directamente a partir de la biblioteca disponible de perfiles de acero que proporciona FAGUS y tomaremos el valor de Ix por defecto sin seleccionar la opción de cálculo por elementos finitos (St. Venant). De este modo el programa nos facilitará el valor procedente del prontuario.
Cuando tengamos una sección compuesta, la modelizaremos mediante elementos de pared delgada y tomaremos el valor de Ix calculado por la fórmula de Bredt (sin seleccionar la opción de St. Venant, aunque, como hemos visto, esto no afecta al valor obtenido) ya que, como hemos visto arriba es el valor que podemos comprobar.
Siempre podremos especificar un valor de Ix distinto al que proporciona FAGUS indicándolo en el campo señalado a continuación:
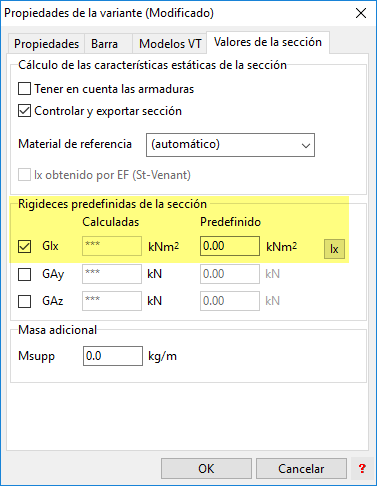
Donde, introduciendo la rigidez torsional GIx, el programa considerará directamente este valor, ignorando el valor de Ix calculado. Esto nos lleva a que el modo más interesante de proceder, si se desea definir una sección con la geometría exacta de los perfiles (y no formada por elementos de pared delgada rectangulares) para emplearla en STATIK, por ejemplo, será introduciendo un modelo de la sección como en el caso 2.a) expuesto arriba (sección introducida mediante contorno poligonal incluyendo un hueco) e introducir manualmente, en el campo señalado en la figura anterior, el valor de la rigidez torsional a partir del Ix obtenido con un modelo auxiliar de pared delgada. Para ello, bastará con multiplicar dicho Ix por el valor de G que estemos considerando para ese material:
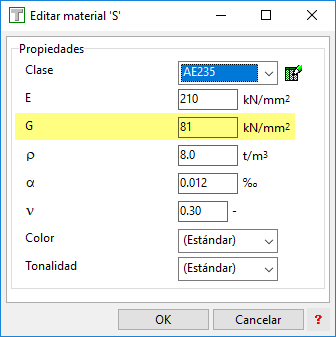
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).

Quizás también te interese:

















