A raíz del segundo reto de la rigidez que planteó Juan Carlos hace tiempo, los compañeros de Cubus Software-España han preparado este superpost. Os dejamos con él.
Una de las muchas novedades que trae el nuevo CEDRUS-8 (pincha aquí para descubrir todas las novedades de la Generación 8) es la posibilidad de considerar la opción de "Rigidez Superestructural" para obtener la bajada de cargas de un edificio (imprescindible disponer del módulo G de edificios).
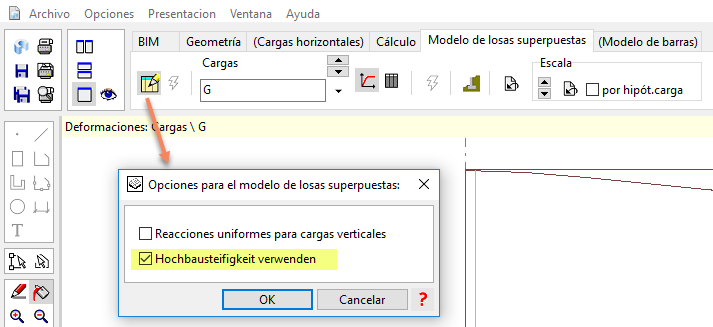
NOTA: Como se observa en la figura anterior, en el momento en el que se redactó este artículo no estaba traducido el texto correspondiente a esta función. La corrección se efectuará en próximas actualizaciones.
Si se activa esta opción, el programa asume la determinación de la rigidez de todos los elementos verticales sin que el usuario intervenga. Se obtendrá, por lo tanto, un modelo de losas superpuestas mucho más refinado en el que la rigidez de cada elemento vertical se determinará a partir de la deformación en su apoyo en la planta subyacente debido a la carga unitaria.
Veremos más adelante, con un ejemplo sencillo, qué efecto tiene esta opción en la bajada de cargas de un edificio, pero antes creemos interesante hacer un pequeño análisis de qué es lo que deberíamos esperar obtener en función de las rigideces de las distintas plantas.
Para evaluar la importancia de la rigidez de los distintos elementos que componen un edificio, en lo que respecta al camino que seguirán las cargas desde la planta superior hasta la cimentación, nos vamos a centrar en el comportamiento que debería tener un pilar apeado que conecta dos plantas en su centro. La geometría podemos verla en la siguiente imagen:
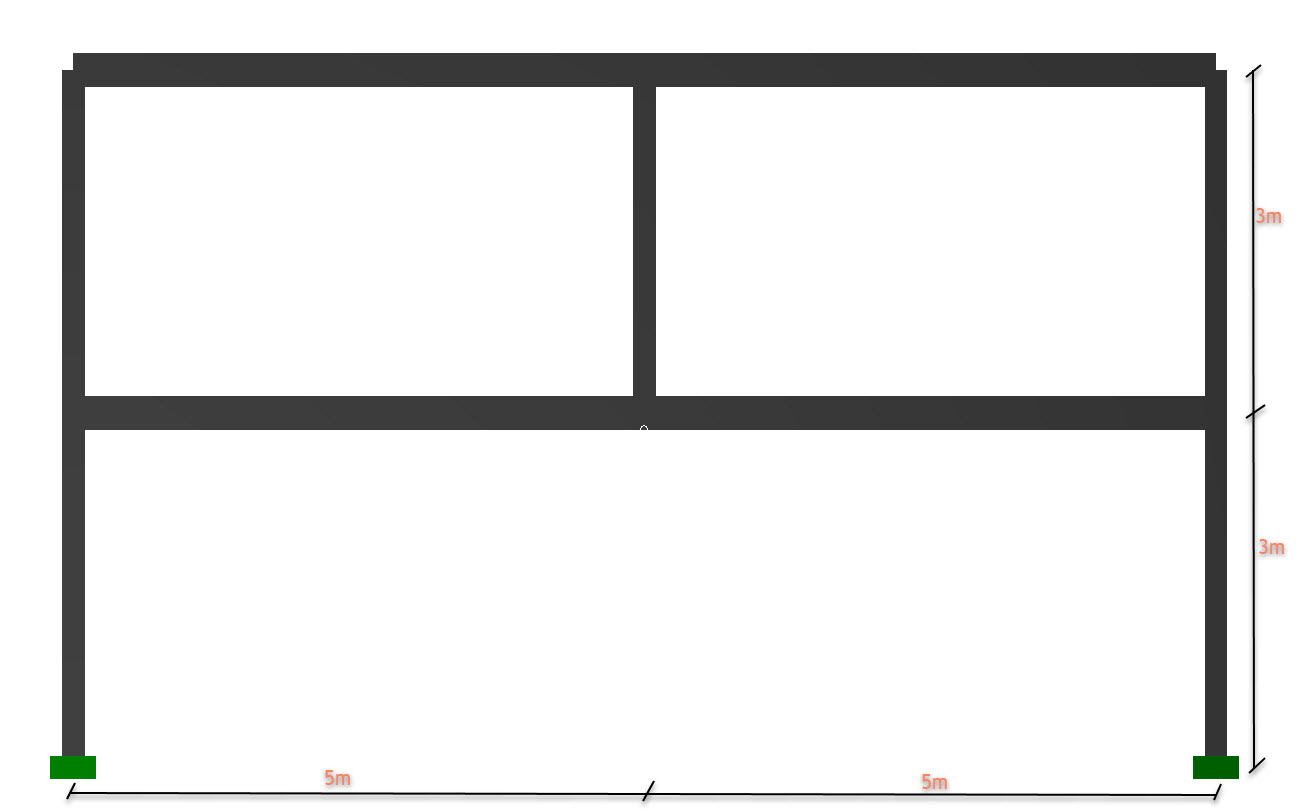
Aplicamos, sobre cada planta, una carga vertical de 5kN/m (nos ayudaremos de nuestro programa STATIK-8 para hacer un modelo de barras auxiliar).
NOTA: Para facilitar la comprensión, en este ejemplo se ha eliminado el peso propio de todos los elementos.
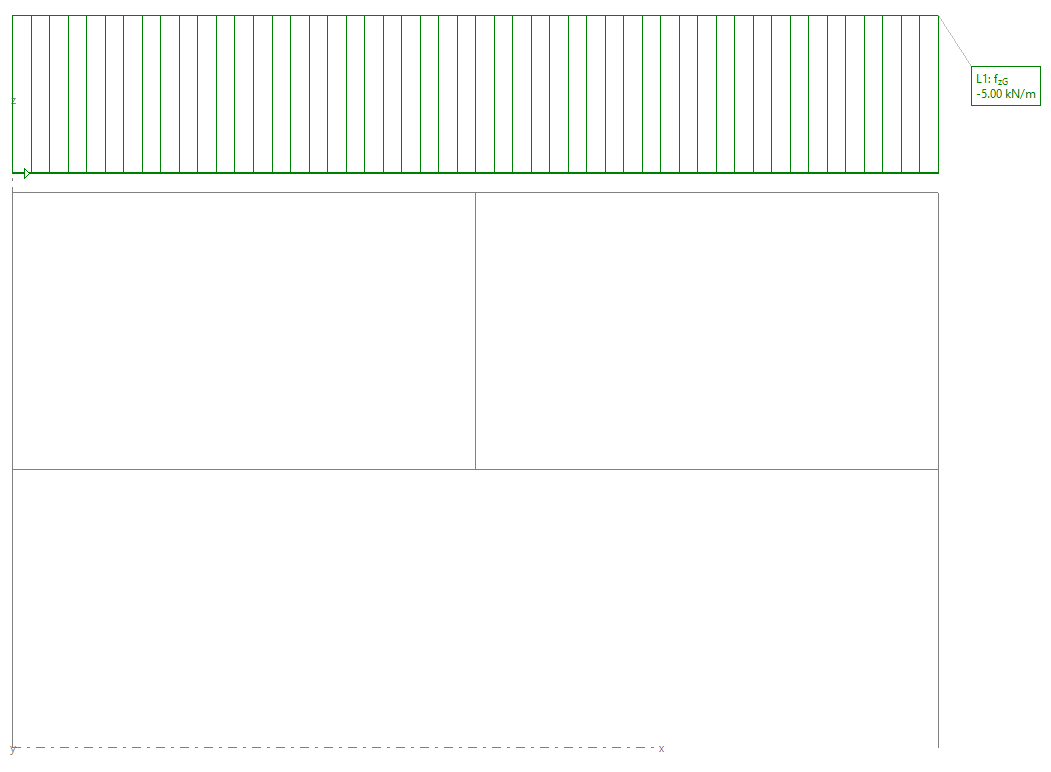
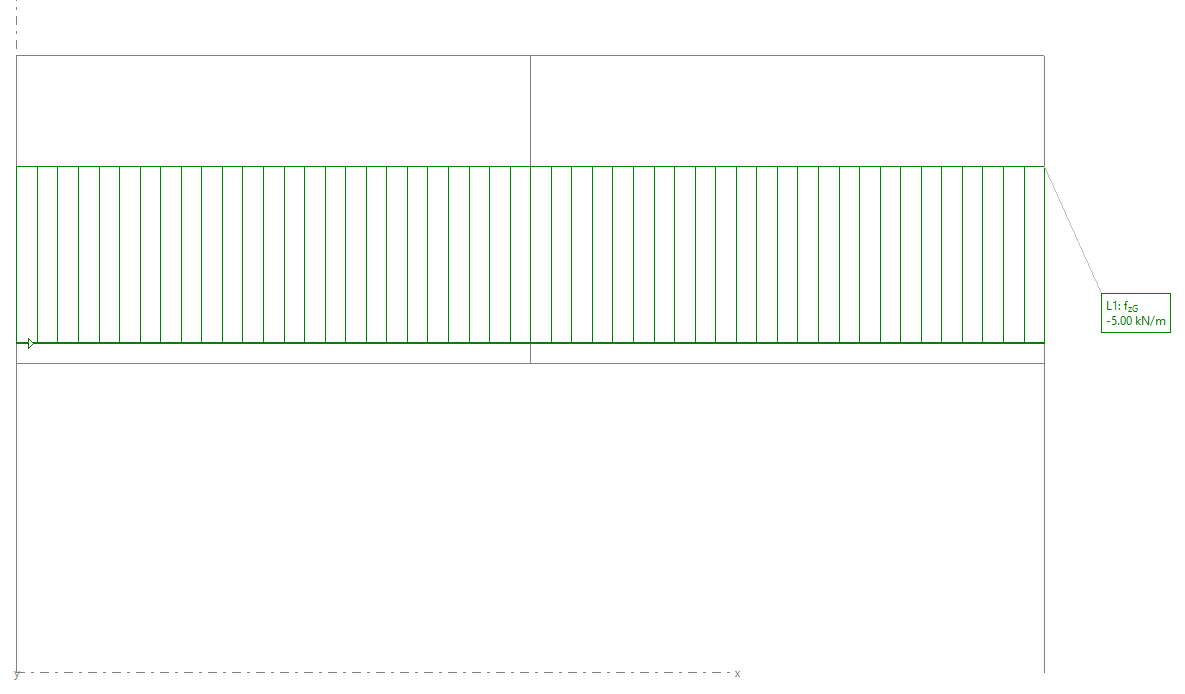
El camino que seguirán las cargas hasta la cimentación es función de las rigideces del sistema estructural.
Vamos a estudiar dos casos muy extremos en cuanto a la rigidez de las plantas:
1- Rigidez de CUBIERTA >>> Rigidez de PLANTA 1
En este caso, la lógica nos dice que las cargas sobre la planta de cubierta bajarán por los soportes extremos. El soporte central no trabajará porque la deformación de la planta 1 será mucho mayor que la deformación de la cubierta.
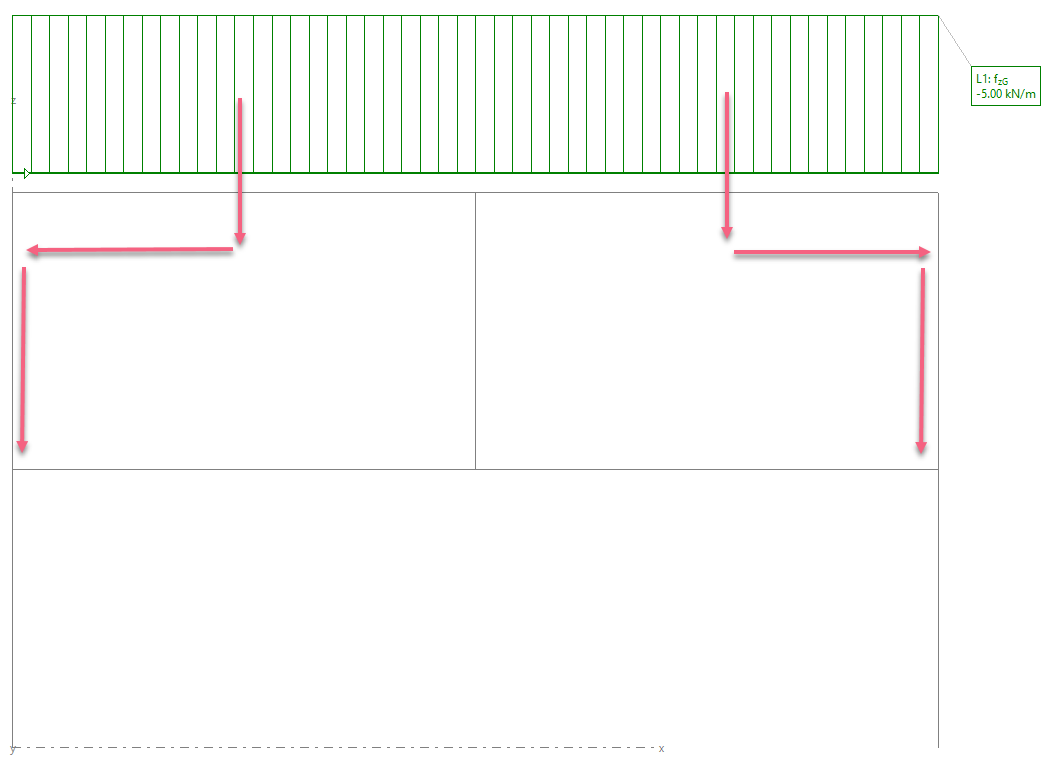
Las cargas de la planta 1 buscarán circular por donde haya mayor rigidez y esto es en la cubierta. Esto hará que una parte de las cargas. en lugar de circular por la planta sobre la que están situadas y que tiene una rigidez muy pequeña, subirán por el soporte central hacia la cubierta para, posteriormente, buscar los soportes extremos y bajar a cimentación. La otra parte de las cargas de la planta 1 bajarán directamente por los soportes extremos.
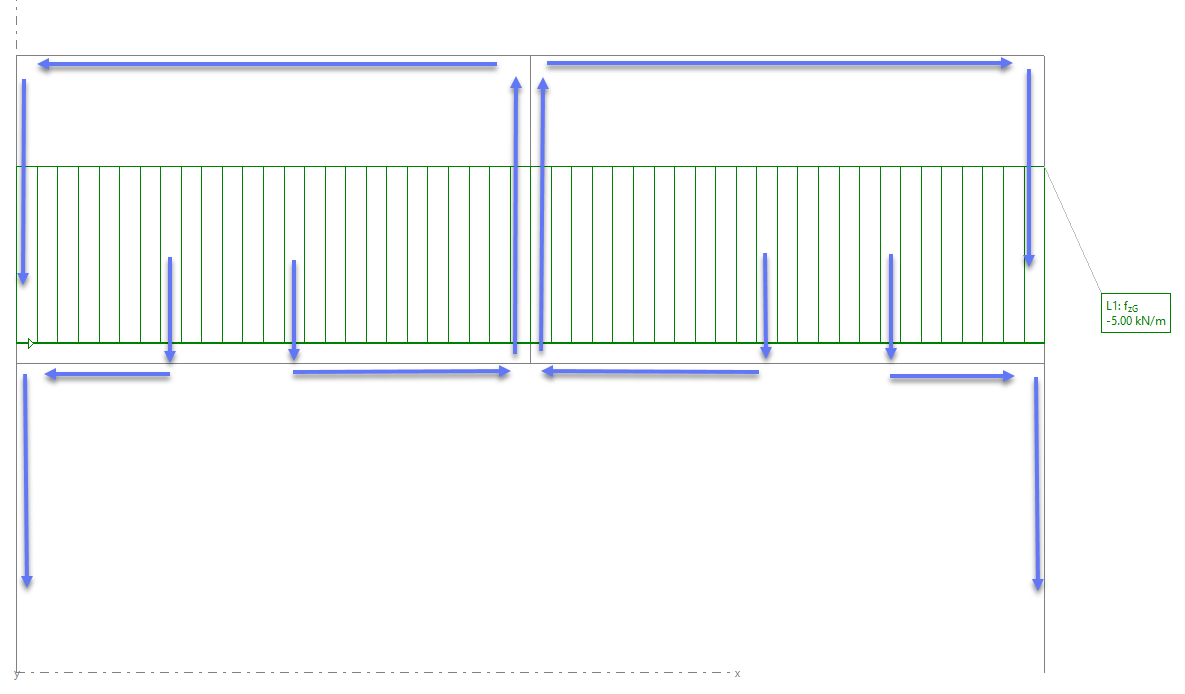
Este comportamiento implicará que el soporte central esté "colgando" de la cubierta en lugar de soportarla, por lo que técnicamente ya **no será un pilar sino un tirante.
Comprobemos lo anterior obteniendo los axiles de cada una de las barras (valores negativos para compresiones y positivos para tracciones). El sumatorio de fuerzas verticales de cada una de las plantas será: 5kN/m*10m= 50kN. Sin considerar la diferencia de rigideces, la planta de cubierta debería descargar 12.5kN en cada soporte extremo y 25kN en el soporte central, mientras que la planta 1 debería descargar 25kN en cada soporte extremo.
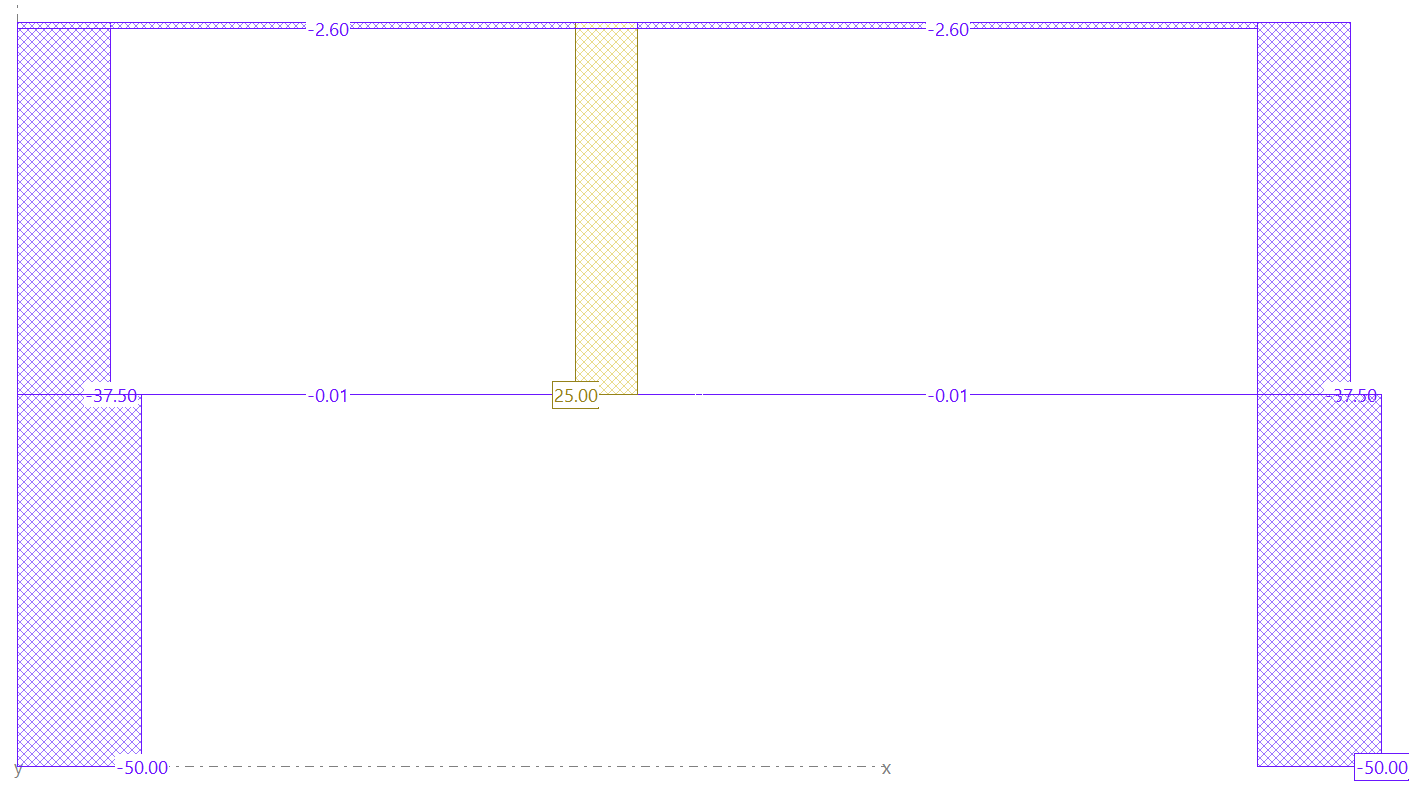
En la figura anterior se observa claramente que la carga de la planta 1 ha subido por el soporte central, implicando una tracción de 25kN. Esta carga, una vez en la cubierta, se ha divido en dos cargas de 12.5kN sobre cada soporte extremo, que sumados a los 25kN resultantes de la bajada de cargas de la propia planta de cubierta, resultan unas compresiones de 37.5kN. La compresión de 50kN de los pilares inferiores indica que están recibiendo la otra parte de carga de la planta 1 que no ha subido por el pilar central.
2- Rigidez de CUBIERTA <<< Rigidez de PLANTA 1
En este caso, cabe esperar que la carga de la planta 1 baje directamente por los soportes extremos, ya que la planta 1 tiene rigidez suficiente para llevar la carga hasta ellos.
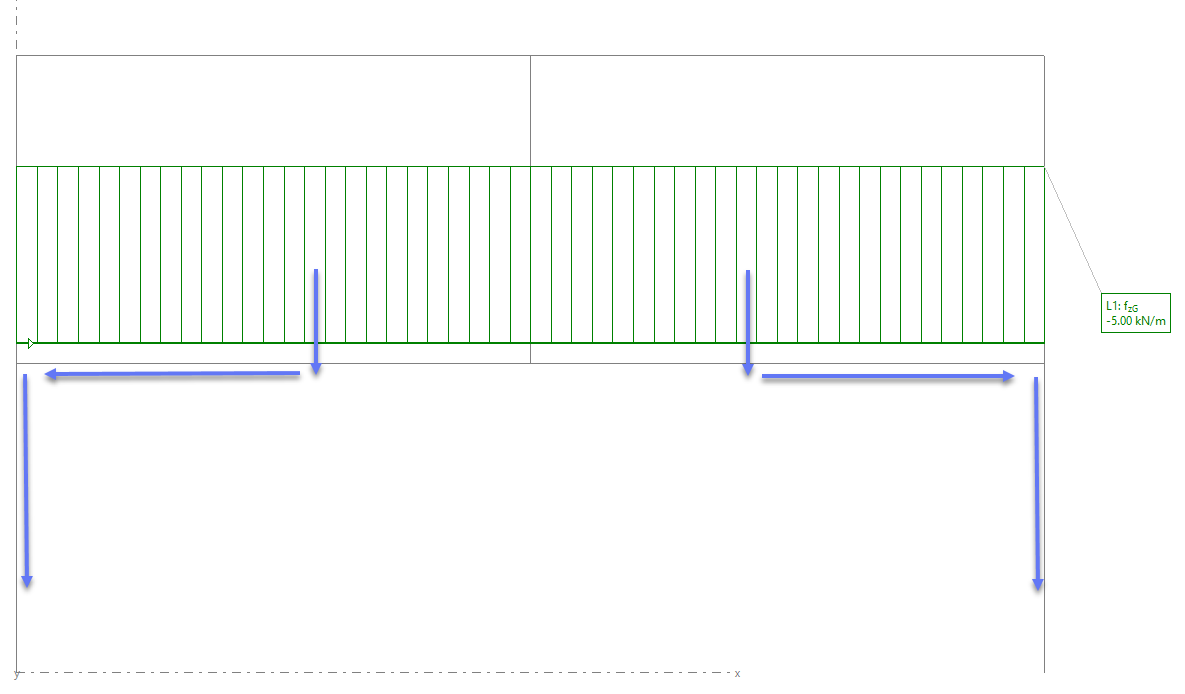
En cuanto a las cargas de cubierta, una parte bajará directamente por los soportes extremos y el resto bajará por el soporte central, para después circular por la planta 1 hasta los soportes extremos.
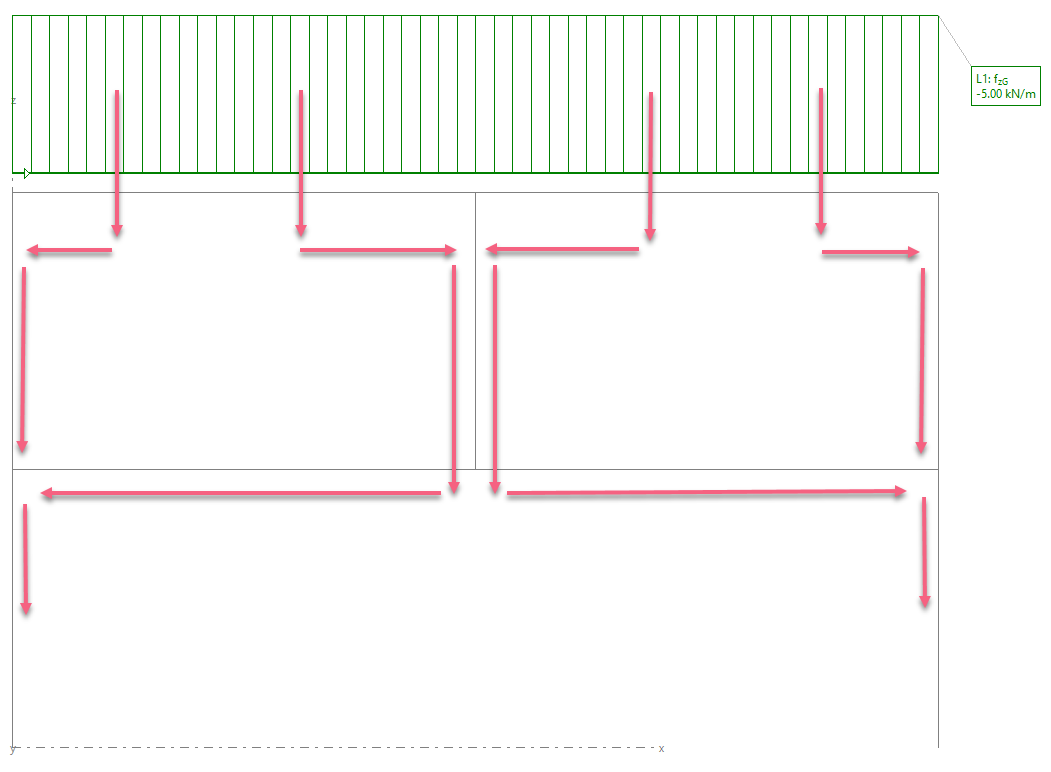
Ahora, el soporte central se comportará como un pilar que sustenta a la cubierta.
Comprobemos lo anterior obteniendo los axiles de cada una de las barras (valores negativos para compresiones y positivos para tracciones). Igual que en el caso anterior, el sumatorio de fuerzas verticales de cada una de las plantas será: 5kN/m*10m= 50kN. La planta de cubierta debería descargar 12.5kN en cada soporte extremo y 25kN en el soporte central, mientras que la planta 1 debería descargar 25kN en cada soporte extremo.
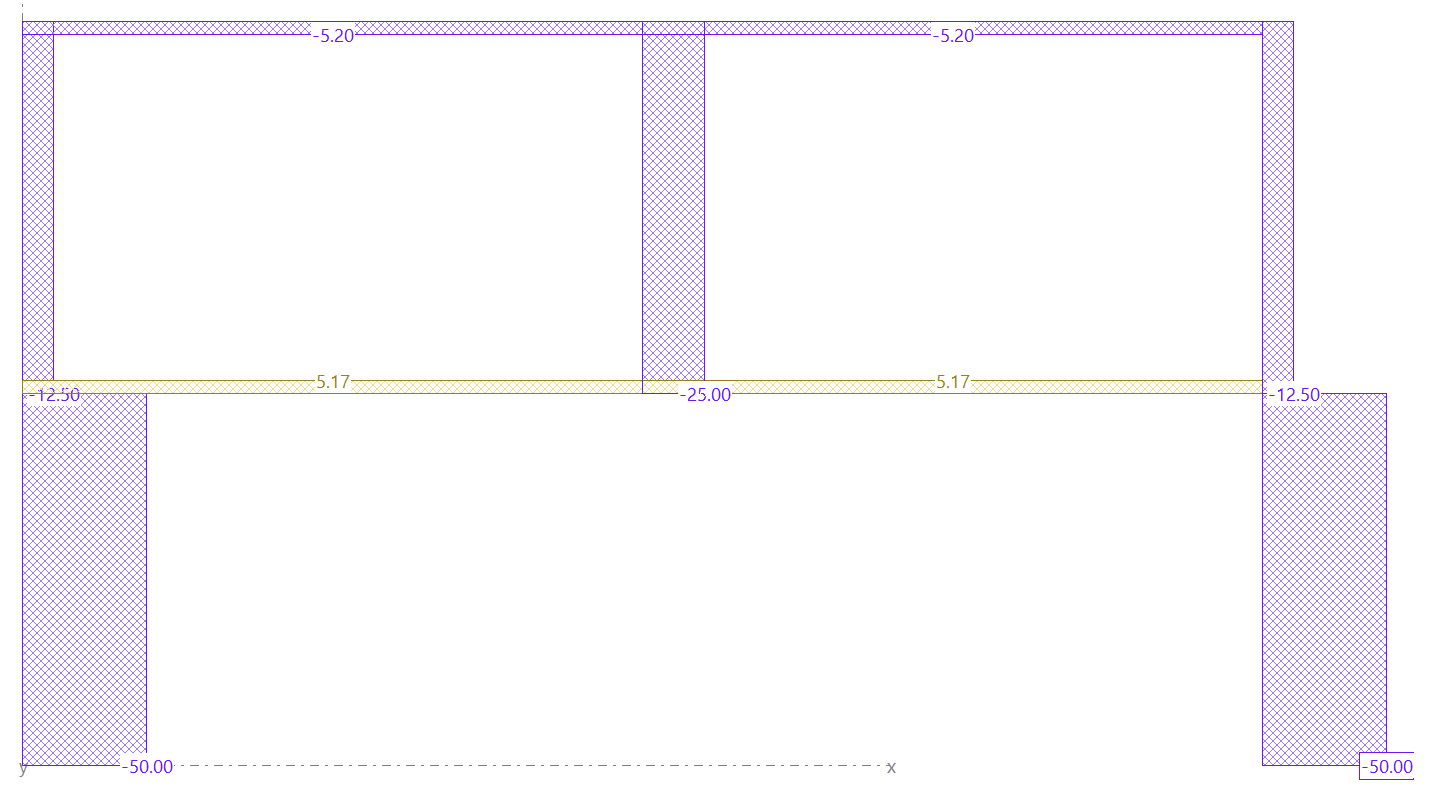
A la vista de los valores de figura anterior se confirma todo lo expuesto anteriormente, siendo destacable el comportamiento, ahora sí, del soporte central como pilar.
Una vez llevado a cabo el análisis anterior, veamos cómo gestiona CEDRUS-8 la bajada de cargas de este mismo edificio utilizando la opción de "Rigidez Superestructural".
Es importante destacar que CEDRUS no permite que los soportes de un edificio trabajen a tracción, por lo que cuando un pilar o un muro deja de estar a compresión, presentará una reacción de valor nulo en su base. Los elementos que ya no estén a compresión no pasarán a trabajar como tirantes sino que, directamente, no formarán parte del sistema de bajada de cargas del edificio. El modelo de losas superpuestas funciona siempre de arriba a abajo y es así el modo en el que se transmiten las cargas de una planta a otra, es decir, siempre de una planta a la subyacente. Como hemos visto, para que un soporte trabaje como un tirante, es necesario que las cargas suban por el mismo hacia la planta superior, comportamiento que no contempla CEDRUS.
Analicemos los distintos casos, sobre el edificio que vemos en la imagen inferior, marcando y desmarcando la opción de "Rigidez Superestructural".
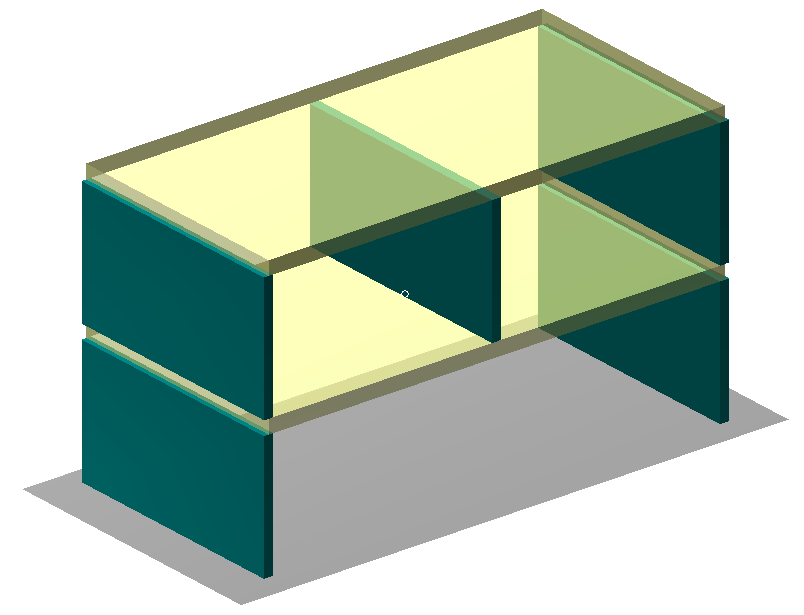
1- Rigidez de CUBIERTA >>> Rigidez de PLANTA 1
- BAJADA DE CARGAS SIN LA OPCIÓN MARCADA
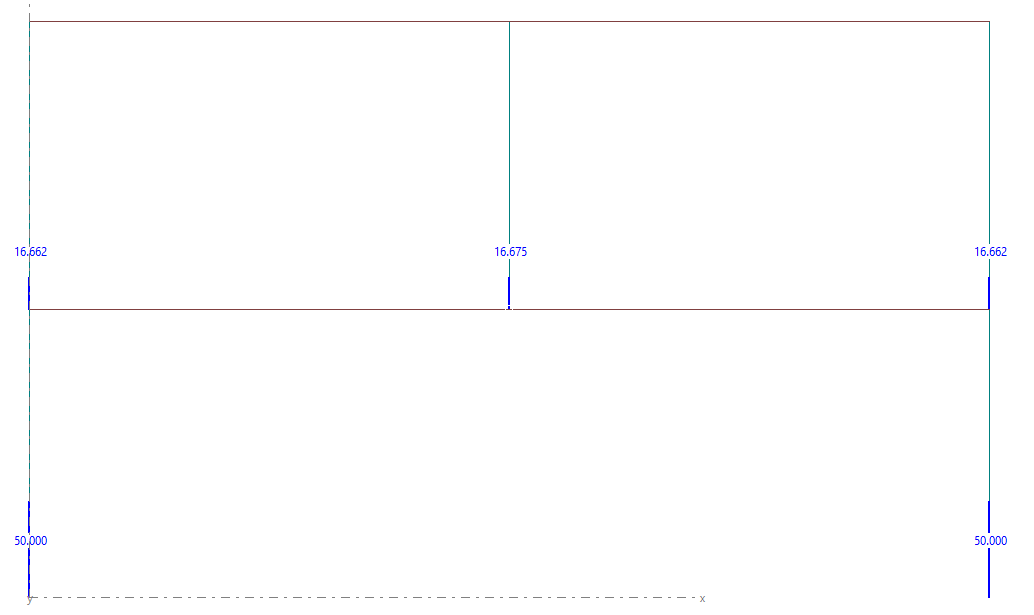
- BAJADA DE CARGAS CON LA OPCIÓN MARCADA
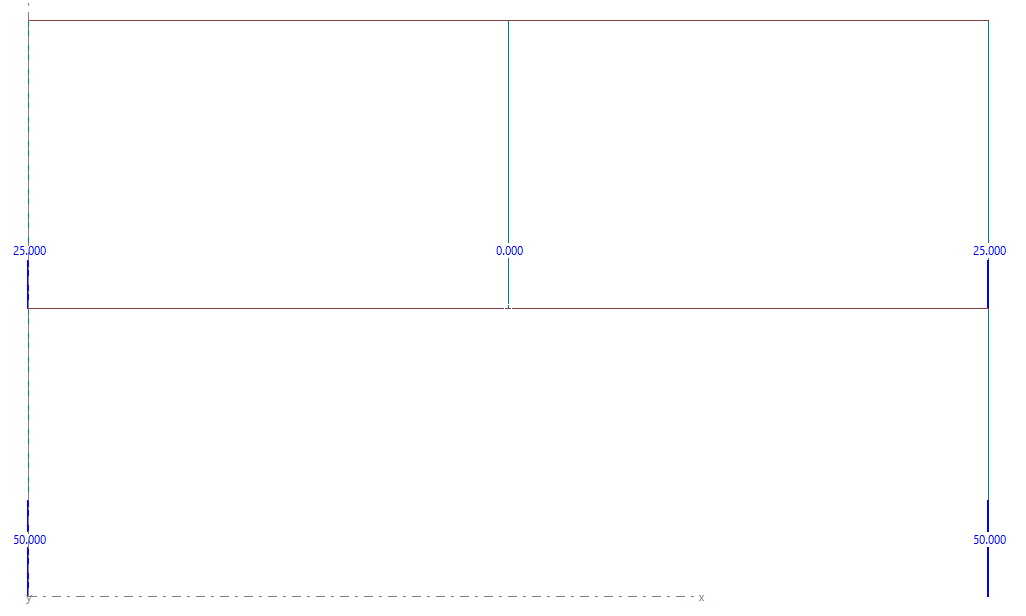
A la vista de los resultados resulta obvio que, cuando marcamos la opción de "Rigidez Superestructural", el programa es capaz de determinar qué camino es el más apropiado para llevar las cargas del edificio hasta la cimentación. Sin la opción marcada tendremos una descarga del pilar central sobre una planta sin rigidez, por lo que la estaríamos penalizando en exceso.
2- Rigidez de CUBIERTA <<< Rigidez de PLANTA 1
En este caso no deberíamos ver diferencia entre marcar y desmarcar la opción porque, en CEDRUS, la rigidez de los elementos verticales dependerá siempre de la rigidez de la planta sobre la que apoyan. En las siguientes imágenes vemos que así es.
- BAJADA DE CARGAS SIN LA OPCIÓN MARCADA
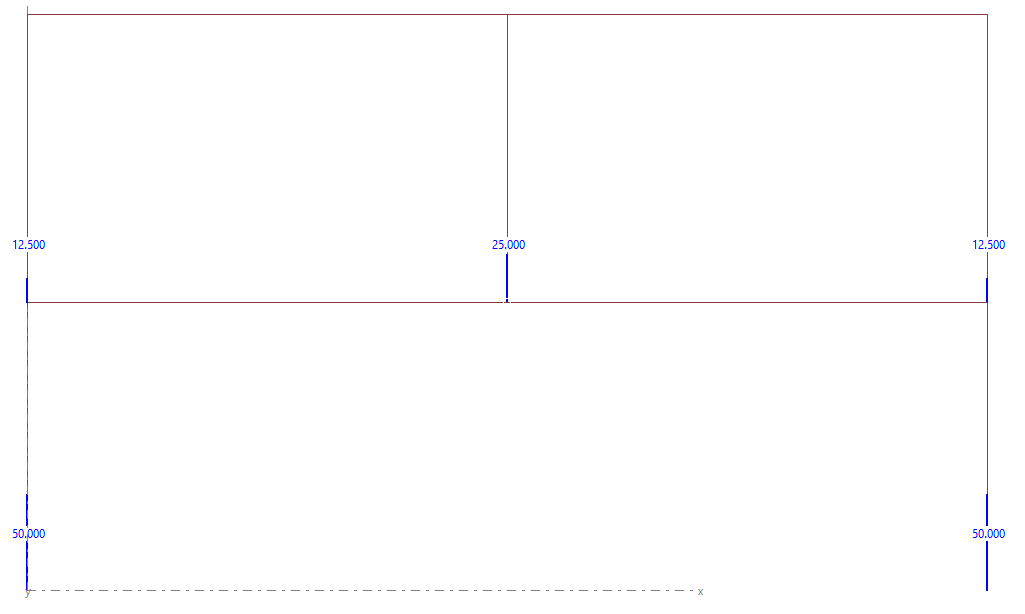
- BAJADA DE CARGAS CON LA OPCIÓN MARCADA

En base a todo lo expuesto en este artículo, concluimos que, en el caso de edificios en los que haya pilares que no llegan a cimentación, es recomendable obtener la bajada de cargas de los edificios marcando la opción de "Rigidez Superestructural". En la realidad no tendremos casos tan extremos como los que hemos presentado a modo de ejemplo en este artículo, ya que en el segundo de los casos, al haber aumentado tanto la rigidez de la losa de planta primera, no se aprecia el efecto de la"Rigidez Superestructural" pero en un caso general sí existirán siempre diferencias entre las rigideces de las plantas que implicarán que haya unos soportes menos cargados que otros.
Si tomamos el mismo edificio con el que estamos trabajando en este ejemplo y no modificamos las rigideces, es decir, dejamos que CEDRUS obtenga las rigideces reales de cada uno de los elementos, veamos qué ocurre marcando y desmarcando esta opción:
- BAJADA DE CARGAS SIN LA OPCIÓN MARCADA

- BAJADA DE CARGAS CON LA OPCIÓN MARCADA
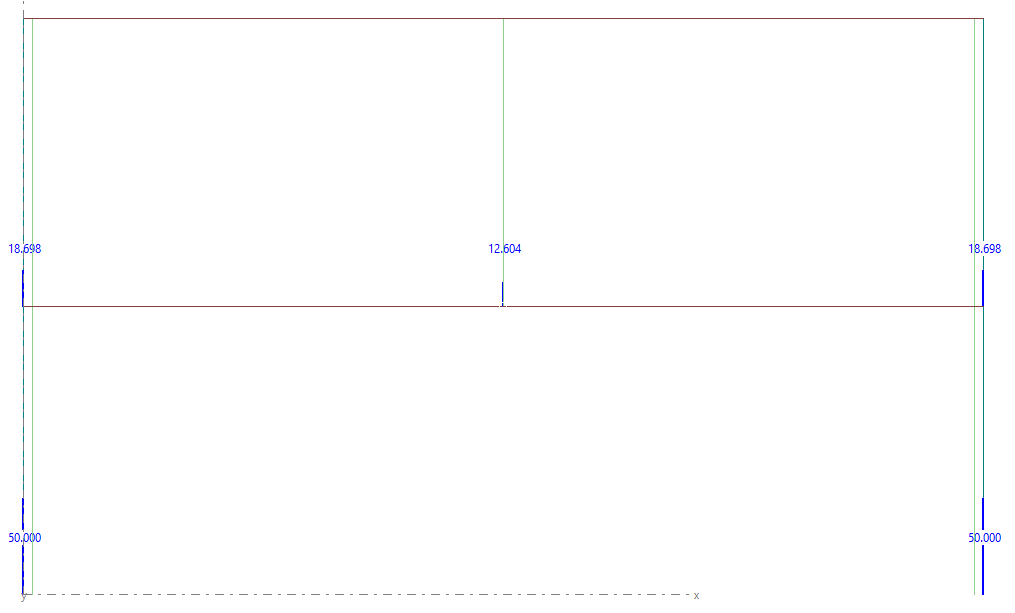
A la vista de los resultados vemos que, efectivamente, seleccionando la opción hacemos que el modelo se comporte de una forma mucho más realista.
Un soporte menos cargado implica una menor solicitación en la planta inferior, teniendo consecuencias directas en su diseño. Esto cobra especial importancia cuando se trata de pilares o muros apeados, cuya carga penaliza notablemente a la planta sobre la que apoya. Si se marca la opción, estaremos, por lo tanto, optimizando el diseño de las plantas.
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).

Quizás también te interese:
















