Hola, sigo clamando por un curso de resistencia de materiales.
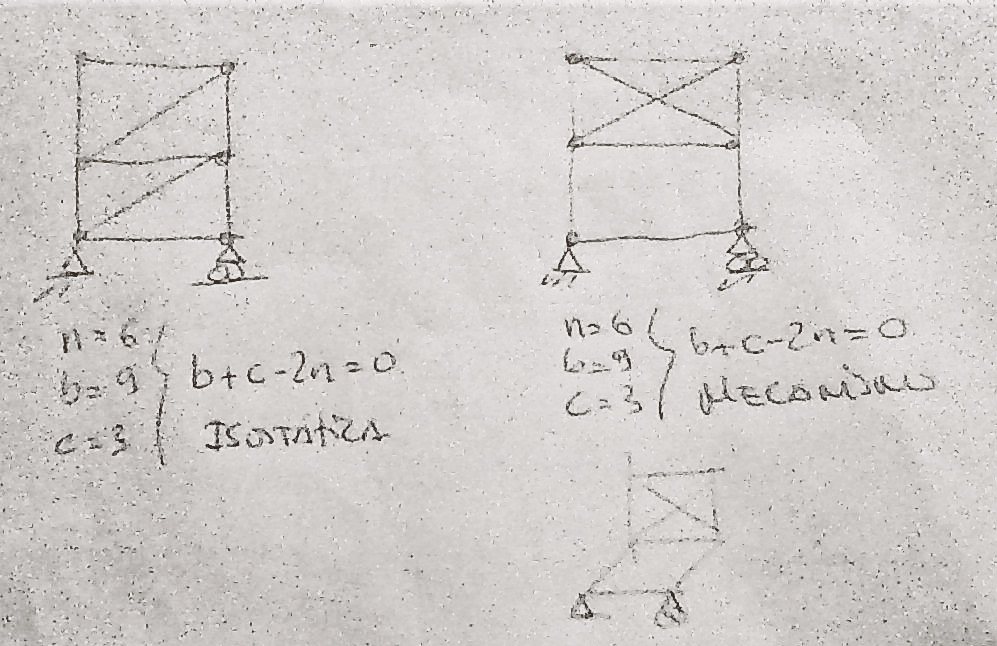
Aparte, no se si alguien me puede sacar de la duda de porque, los grados de libertad internos de una estructura de barras es 3*(n-1), de donde sale esa formula? Un saludo y muchas gracias!!!!!
Aparte, no se si alguien me puede sacar de la duda de porque, los grados de libertad internos de una estructura de barras es 3*(n-1), de donde sale esa formula? Un saludo y muchas gracias!!!!!